WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte kruis

Hallo,

In een vierkant van 10 bij 10 cm wordt een gekleurd kruis getekend. Iedere arm van dit kruis is x cm lang.
Leg uit dat de armen van het kruis 10-2x cm breed zijn.
Ik begrijp het antwoord niet: Als je naar een zijde van het grote vierkant kijkt zie je dat de 10 cm is opgedeeld in 2X x cm en de breedte van een arm van het kruis. Voor die breedte blijft dus 10-2x cm over. Maar je hebt toch ook een middenstuk, dus dat kan nooit je gehele lengte zijn.
Die begrijp ik wel
Leg uit dat voor de totale oppervlakte van het gele deel geldt W=4x²+(10-2x)².
De totale oppervlakte van het vierkant is 100. Toon met de formules voor K en W aan dat voor elke waarde van x geldt dat de oppervlakte 100 is, dus K+W=100. De formule van K kreeg je bij vraag B en dat is K=40x-8x²
Bereken de exacte waarde van x waarbij K en W gelijk zijn
Bereken met de rekenmachine voor welke waarden van x de totale oppverlakte van het gele gebied vier keer zo groot is als de totale oppervlakte van de armen van de kruis.
Ook deze vraag begrijp ik niet wat ze eigenlijk vragen.
Alvast hartelijk bedankt

Lilian
Leerling bovenbouw havo-vwo - zondag 17 oktober 2010

Antwoord

A.
De zijde van het vierkant is 10, de lengte van een 'arm' is x. Er blijft dan 10-2x over voor de breedte.

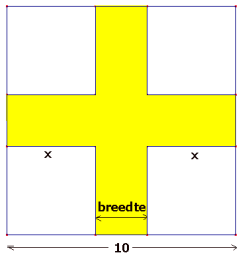
Lijkt me geen probleem...

C.
De gegeven formule klopt niet.

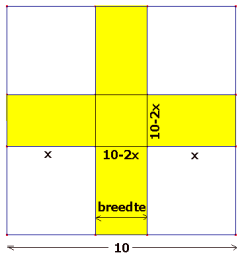
Dus:
K = 4·x·(20 - 2x)+(10 - 2x)²
K = 100 - 4x²

D.
W = 4x²
K + W = 100 inderdaad!

E.
Los op: 4x² = 50

F.
Er geldt: K = 4·W, dus:
Los op: 100 - 4x² = 4·4x²

Helpt dat?

Naschrift

Maar waarschijnlijk bedoelde je iets anders?!

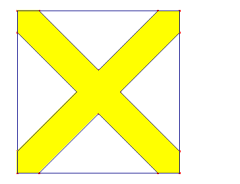
Dat kan ook...
K=100-2x²
W=2x²
..en dan klopt die 10-2x niet...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 17 oktober 2010