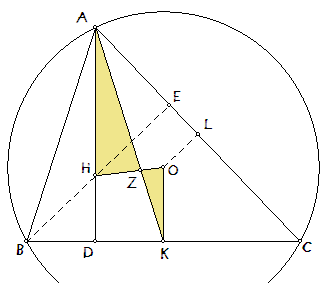WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Driehoek en negenpuntscirkel

Dit is een reactie op vraag 61553

Wat is het bewijs van die eigenschap van het punt O?
Stijn
Overige TSO-BSO - zondag 17 oktober 2010

Antwoord

In onderstaand plaatje zijn K en L middens van de zijden BC en CA van driekoek ABC. O is het middelpunt van de omgeschreven cirkel van driehoek ABC.

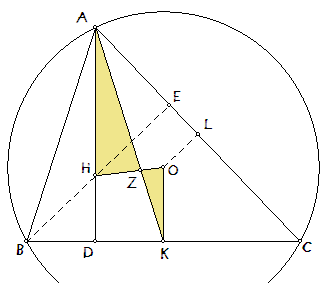
AK is dan zwaartelijn. En zoals bekend, ligt het zwaartepunt Z zo op die lijn dat AZ : ZK = 2 : 1.
We bekijken nu de homothetie (vermenigvuldiging) met Z als centrum en factor -2.
Dan wordt K op A afgebeeld. En O op een punt H. De rechte OK staat loodrecht op BC, zodat ook de rechte AH (het beeld van de rechte OK) loodrecht staat op BC (immers de beeldrechte van een rechte bij een homothetie is evenwijdig met het origineel).
AH is dus hoogtelijn.
En ook is duidelijk (vanwege de homothetie), dat AH = 2 · OK .
Nu nog te bewijzen dat H inderdaad het hoogtepunt is van driehoek ABC.
Ook de rechte OL wordt door de homothetie afgebeeld op een hoogtelijn (namelijk op BE).
En dan is direct duidelijk dat H als snijpunt van die lijnen het hoogtepunt van driehoek ABC is.

We hebben dus de eigenschap:
De afstand van het middelpunt van de omgeschreven cirkel van een driehoek tot een zijde is gelijk aan de helft van het 'bovenste stuk' van de hoogtelijn op die zijde.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 17 oktober 2010