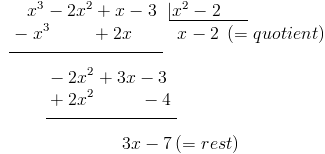WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Euclidisch delen

Hoi,
Ik ga volgend jaar naar het vijfde middelbaar, maar omdat ik van 4u naar 6u wiskunde ga, moet ik een pakket bijwerken rond euclidisch delen. Ik heb al van alles geprobeerd, maar sommige oefeningen willen niet lukken.
Dus mijn vragen :
Ik kan euclidisch delen, maar bij deze oefening loopt het steeds mis : 'Deel f(x) = x³-2x²+x-3 door x²-2'.
Zou u mij hierbij kunnen helpen ?
Nu heb ik nog een laatste vraag : zou u mij op weg kunnen zetten met de volgende oefening : 'Bij deling van f(x)= 2x³+ax²+bx-3 door x+1 en door x+3 is de rest telkens 0. Bepaal a en b.' ?

Alvast bedankt,
Sofie
Sofie
2de graad ASO - vrijdag 13 augustus 2010

Antwoord

Hallo

De uitwerking van de eerste deling :

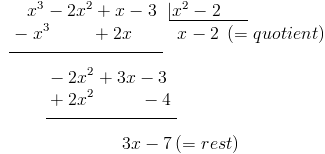
Bij de tweede oefening maak je gebruik van de reststelling :
De rest van de deling van een veelterm door x-a vind je door in de veelterm x te vervangen door a.
Om de rest van de deling door x+1 te kennen moet je dus x vervangen door -1.
Vermits deze rest gelijk is aan nul bekom je :
-2 + a - b - 3 = 0 of a - b = 5
Voor de rest van deling door x+3 te kennen moet je dus x vervangen door -3:
-54 + 9a - 3b - 3 = 0 of 9a -3b = 57
Uit dit stelsel van deze twee vergelijkingen kun je a en b berekenen.
Je vindt : a = 7 en b = 2

Lukt het zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 13 augustus 2010