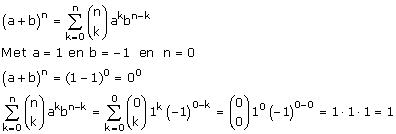|
|
|
\require{AMSmath}
Re: Binomium van Newton
Beste mensen,
Bedankt voor het antwoord. ik had inderdaad zitten goochelen met de binomiaalcoefficienten.
Maar nog ben ik er niet helemaal uit, want wat als je mbv het binomium van Newton deze som moet berekenen, en zelf de waarden van a en b moet kiezen:
Sn (n) (-1)k
k=0 (k)
a is dan 1, b=-1, dus (a+b) wordt verheven tot de n-de macht. Dwz dat (1-1)=0 wordt verheven tot de n-de macht. De som is dan altijd 0, behalve als n=0, want dan wordt 0 verheven tot de 0de macht en dat is volgens afspraak 1.
Of redeneer ik nu verkeerd? Het modelantwoord luidt 0.
Nogmaals dank!
Lisi
Lisi R
Cursist vavo - vrijdag 16 juli 2010
Antwoord
Grappig wel. Als ik alles 'gewoon invul' dan zou ik denken dat je gelijk hebt:
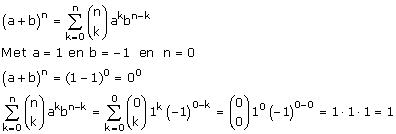
...dus kennelijk is die afspraak (?) niet zo gek...
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 16 juli 2010
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 62827