WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ontbinden in factoren

Ik kom er niet uit bij het ontbinden van factoren en dan het buiten halen van van de haakjes. met een voorbeeld k²+k-42 dat lukt mijn niet ik zou het graag willen dat u mij zou helpen nog een voorbeeld k³-4k en k³+5k²+4k

En het zou nog van pas komen als er zo snel mogelijk een uitleg voor kan worden gegeven want, ik heb het wel gelezen op jullie site maar begrijp het nog steeds en ik heb namelijk woensdag de 9-04-2003 een repetitie hartelijk bedankt alvast
elly d
Leerling bovenbouw havo-vwo - zondag 6 april 2003

Antwoord

'Normaal' gesproken zijn er twee soorten van ontbinden in factoren:
Een zo groot mogelijke term buiten haakjes halen.
Van een drieterm een produkt van 2 tweetermen maken.
Deze laatste soort staat wel bekend onder de naam produkt-som methode of som-produkt methode.

Voorbeeld
x² + 8x + 12 kun je ontbinden als (x + 6)(x + 2).
Controle:
(x + 6)(x + 2) = x² + 2x + 6x + 12 = x² + 8x + 12
Klopt!

De vraag is nu: hoe kun je zo'n ontbinding vinden?
Laten we eens kijken naar wat voorbeelden:

(x + 2)(x + 3) = x² + 5x + 6
(x + 2)(x-3) = x² - x - 6
(x + 1)(x - 4) = x² - 3x - 4
(x - 4)(x - 4) = x² - 8x + 16
(x - 3)(x + 3) = x² - 9

Als het goed is vallen er twee dingen op:
Het getal voor de x aan de rechter kant is de som (optellen dus) van de twee getallen aan de linker kant.
Het getal aan de rechter kant is het produkt (vermenigvuldigen dus) van de twee getallen aan de linker kant.

Schematisch:

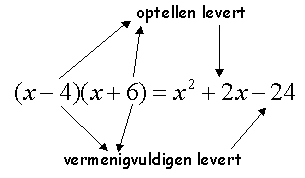
Nu andersom:

Je wilt een ontbinding vinden voor x² + 7x + 12
Op grond van het bovenstaande moet je twee getallen zoeken die opgeteld 7 zijn en vermenigvuldigd 12.
Mogelijke kandidaten (alle mogelijke tweetallen met als produkt 12):

Produkt
1 · 12
2 · 6
3 · 4
-1 · -12
-2 · -6
-3 · -4

Als je nu ook nog naar de som kijkt, krijg je volgende tabel:

Produkt Som
1 · 12 13
2 · 6 8
3 · 4 7
-1 · -12 -13
-2 · -6 -8
-3 · -4 -7

Ik zocht twee getallen met produkt 12 en som 7, dus 3 en 4.
Je kunt x² + 7x + 12 dus ontbinden als (x + 3)(x + 4)

Vaak is het niet nodig (of zelfs verstandig) om zo'n tabel te maken. Als je goed kijkt (en nadenkt)
kun je het soms zo zien.

k²+k-42:
Met de produkt-som-methode! We zoeken twee getallen die opgeteld 1 zijn en vermenigvuldigd -42. Mogelijk kandidaten zijn:
1·-42 de som is -41
2·-21 de som is -19
3·-14 de som is -11
6·-7 de som is -1
...maar ook:
-1·42 de som is 41
-2·21 de som is 19
-3·14 de som is 11
-6·7 de som is 1
Ah.. de laatste is het!
Dus k²+k-42=(k-6)(k+7)

k³-4k
Dit is een typisch geval van k buiten haakjes halen! Dus schrijven we:
k³-4k=k(k²-4)

Nu bestaat er ook nog zoiets als het merkwaardig produkt!? (zie zoeken). Eén van die merkwaardige produkten zegt:
a²-b²=(a+b)(a-b)
Toegepast op k(k²-4) krijg je dan nog:
k³-4k=k(k²-4)=k(k+2)(k-2)

Je kunt hierbij ook denken aan de produkt-som-methode! Ik zoek twee getallen die opgeteld nul en vermenigvuldigd -4 zijn. Dat zijn -2 en 2.
k³+5k²+4k
Ook hier kan je een 'k' buiten haakjes halen. Dus schrijven we:
k³+5k²+4k=k(k²+5k+4)

Voor het deel tussen de haakjes kan je de produkt-som-methode gebruiken:
k²+5k+4
Ik zoek weer twee getallen die opgeteld 5 en vermenigvuldigd 4 zijn. Dat zijn 1 en 4.
Dus:
k³+5k²+4k=k(k²+5k+4)=k(k+4)(k+1)

Hopelijk kan je zelf verder. Kijk ook even op onderstaande website voor meer voorbeelden!
Zie Ontbinden in factoren

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 6 april 2003