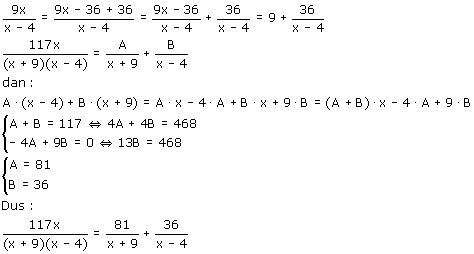|
|
|
\require{AMSmath}
Ontbinding van derdegraadsvergelijking
Bedankt voor het antwoord op mijn vraag "oplossen van deze gebroken vergelijking".
Nu weet ik dat er geen oplossing is, hoe dat ik dat op mijn taak van Wiskunde tegen na de vakantie, ga schrijven, weet ik nog niet!!!
Maar hoe kom je aan de ontbinding van de derdegraadsvergelijking x3+14x2+9x-324=0, wat (x-4)(x+9)2 bleek te zijn. Want voor de ontbinding van vierkantsvergelijking heb je toch ook eerst de oplossingen nodig?!
En waarom is (9x):(x-4)=((36):(x-4))+9
en is (117x):((x+9)(x-4))=((81):(x+9))+((36):(x-4))
Misschien een "voor de hand liggend" antwoord, maar ik zou het toch graag te weten komen.
Elke D
2de graad ASO - maandag 30 december 2002
Antwoord
Je hebt gelijk. De gegeven oplossing ligt niet erg voor de hand. Op zich is het wel te begrijpen, maar kom er maar eens op:
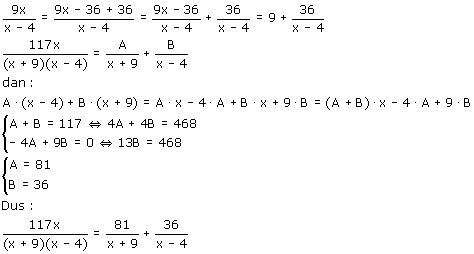
Maar ja, dat gaat misschien wel wat ver.
Ik zou zeggen: hou je bij je eigen methode. Kennelijk is het mogelijk dat je daarbij op een derdegraadsvergelijking uitkomt. Als je geluk hebt kan je die dan ontbinden in factoren.
We hadden gevonden: x3+14x2+9x-324=0. En hoe los je dat op? Tja... het zal zoiets moeten worden als (x+..)(x+..)(x+..). Omdat 324=22·34 zou je het eens kunnen proberen met (x-4)?x-4/x3+14x2+9x-324\x2+18x+81
x3-4x2
-----
18x2+9x-324
18x2-72x
--------
81x-324
81x-324
-------
0 x3+14x2+9x-324=(x-4)(x2+18x+81)=(x-4)(x+9)2
Maar ik geef toe het is een beetje prutsen geblazen. In de database staan meer voorbeelden.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 31 december 2002
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 6216