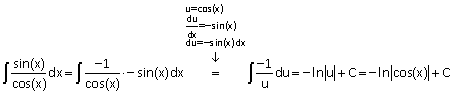WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Primitieve goniometrie functies

hallo,

ik had een paar vragen over de primitieve van een paar goniometrische functies.

ik denk mijn probleem is, ik ken de basis niet vandaar dat ik steeds vast zit. Dus dacht ik, ik wil eerst de basis primiteve weten van een paar goniometrische funsties.

Ik weet al:

sin(ax+b)= -1/a.cos(ax+b)
cos(ax+b)= 1/a.sin(ax+b)
tan(x)= ( dat weet ik niet)

en wat is de primitieve als de functies als ze in het kwadraat zijn? Dus bijv.: 3sin²(3x)?
Kan ik hier kettingregel gebruiken?

En er is een vast regel denk ik voor het primitieve van: 1/cos²(2x)? maar die ken ik ook niet en ze staan niet in de formule kaart...

ik hoop dat u mij kan helpen.

gr. anja
Anja
Leerling bovenbouw havo-vwo - vrijdag 2 april 2010

Antwoord

Een paar tips dan maar.

$
f(x) = \tan (x)
$ kan je schrijven als $
f(x) = {{\sin (x)} \over {\cos (x)}}
$. Met de substitutiemethode kan je dan laten zien dat:

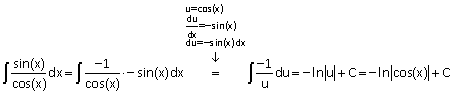
Bij $
f(x) = 3 \cdot \sin ^2 (3x)
$ kan je gebruik maken maken van:

$
\cos (2x) = 1 - 2\sin ^2 x \Rightarrow \sin ^2 x = {1 \over 2} - {1 \over 2}\cos (2x)
$

Je krijgt dan:

$
\int {3 \cdot \sin ^2 (3x)\,dx = \int 3 } \cdot \left( {{1 \over 2} - {1 \over 2}\cos (6x)} \right)\,dx = \int {1{1 \over 2}} - 1{1 \over 2}\cos (6x) dx
$

..en dan zal 't wel lukken.

Bij $
f(x) = {1 \over {\cos ^2 (2x)}}
$ kan je de afgeleide van f(x)=tan(x) herkennen? Lukt het dan?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 2 april 2010