|
|
|
\require{AMSmath}



Sinus en cosinus
Als cos x=p, wat is x dan, en als sin x=p, wat is x dan.
(In p uitgedrukt)
inge v
Leerling bovenbouw havo-vwo - zondag 29 december 2002
Antwoord
Beste Inge,
Voor p Î  kan de uitkomst enkel en alleen tussen -1 en 1 liggen, aangezien de cosinus en sinusfunctie enkel gedefinieerd is tussen -1 en 1. kan de uitkomst enkel en alleen tussen -1 en 1 liggen, aangezien de cosinus en sinusfunctie enkel gedefinieerd is tussen -1 en 1.
Je wilt dus weten welke waarde je moet nemen voor de sinus of cosinus waar een gegeven getal p voor uitkomt (zie onderstaande opmerking).
Hiervoor heb je de inverse functie voor nodig (bv. worteltrekken en kwadrateren = inverse bewerking).
De inverse bewerking van sinus = arc(us) sin (ookwel boogsin, sin-1, inv sin, ...).
De inverse bewerking van cosinus = arc(us) cos (ookwel boogcosinus, cos-1, inv cos, ...).
Die inverse bewerking kun je berekenen m.b.v. je rekenmachine, er zal op je rekenmachine iets staan zoals inv sin, sin-1, ...
Je rekenmachine zal één waarde geven, maar aangezien de functie periodiek is kun je er een veelvoud van 2p bij optellen of aftrekken. Maar de inverse functie is enkel gedefinieerd tussen -1 en 1 (zie bovenstaande regels), dus je gekozen p moet tussen -1 en 1 liggen.
Een andere manier is twee functies te plotten, één functie is de cosinus of sinusfunctie (naargelang je cos x = p, of sin x = p wilt berekenen), en de andere functie, is de rechte y = p. Het snijpunt van de twee functies is de waarde van x, hetgeen overeenkomt met de inverse functie.
Je kunt dat snijpunt vinden via je grafische rekenmachine (met Casio via intersect), of via een software-pakket zoals Maple. Hieronder zie je een figuur gemaakt met Maple, om sin x = 0,5 of cos x = 0,5 te bepalen.
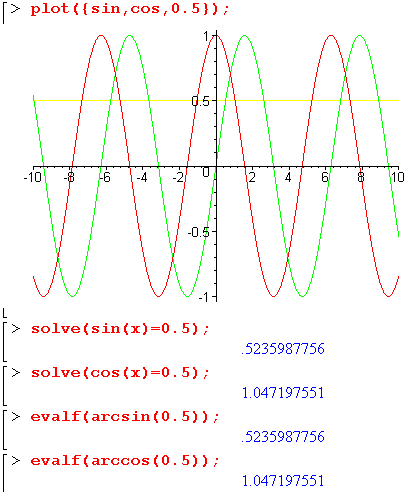
Hopelijk is het nu duidelijk,
Groetjes,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 29 december 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 kan de uitkomst enkel en alleen tussen -1 en 1 liggen, aangezien de cosinus en sinusfunctie enkel gedefinieerd is tussen -1 en 1.
kan de uitkomst enkel en alleen tussen -1 en 1 liggen, aangezien de cosinus en sinusfunctie enkel gedefinieerd is tussen -1 en 1. 

