WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Raaklijnen

Gegeven een scherphoekige driehoek ABC, de verlengde zwaartelijn uit A snijdt de omgeschreven cirkel in D.
De raaklijn in A aan de omgeschreven cirkel snijdt het verlengde van de zijde BC in P. De raaklijn in D aan de omgeschreven cirkel snijdt het verlengde van de zijde CB in Q. Hoe bewijs ik dat PA = QD ?
G.Jaco
Ouder - maandag 25 januari 2010

Antwoord

Beste G.
Ik weet niet of dit de mooiste manier is om het te bewijzen.
In het plaatje is Z het midden van BC en M het middelpunt van de cirkel door A,B en C.
De rode cirkels gaan door A,M,D en door D,Z,M.

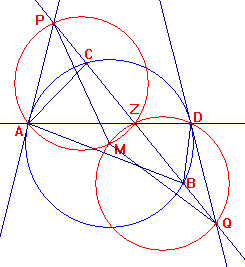
Je kan bewijzen dat die twee rode cirkels even groot zijn.
Hoek AZM staat op boog AM in cirkel door A,Z,M en op boolg MD in de cirkle door D,Z en M.
Omdat AM=MD (stralen) zijn ook de rode cirkels gelijk.
Hoek MZQ is hoek MDQ=90 graden.Immers M op middelloodlijn van BC.Daarom ligt Q ook op de cirkel door D,Z en M.
Hetzelfde geldt voor MZP en MAP, zodat P op de cirkel door A,Z en M ligt.
De rest is dan niet zo moeilijk meer.
Ik hoop dat dit duidelijk is.
Groet,
Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 25 januari 2010

Re: Raaklijnen