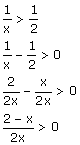|
|
|
\require{AMSmath}



Een ongelijkheid oplossen
Het gaat zich om de volgende opgave.
1/x $>$ 1/2
Ik moet de uitkomsten vervolgens in een van de volgende schema's invullen:
x ... x$>$.. of .. ... x$>$.. of .. x x .. ..
Ik was zelf zo ver gekomen.
Kruislings vermenigvuldigen geeft:
1/x $>$ 1/2 $\to$ x$>$2
tom w
Student hbo - woensdag 20 januari 2010
Antwoord

Er zijn (zullen we maar zeggen) drie verschillende manieren om deze ongelijkheid op te lossen. Elke methode vraagt al dan niet meer of minder inzicht, intellectuele inspanning en vaardigheden.
1.
De functie f(x)=1/x is een standaardfunctie. Als het goed is weet je hoe die grafiek er uit ziet. Wanneer is 1/x=1/2? Bij x=2.
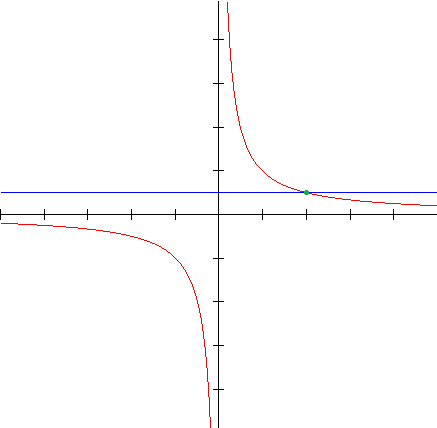
De vraag wanneer is f(x)$>$1/2 laat zich nu beantwoorden.
Het antwoord is 0 x x 2 2
2.
In het voortgezet onderwijs is het gebruikelijk om gebruik te maken van een grafische rekenmachine. Plot de grafiek van f(x)=1/x en de grafiek van g(x)=1/2. Bereken (of lees af) de co÷rdindaten van de snijpunt(en) en beantwoord de vraag opdezelfde manier als 1.
Het berekenen van de snijpunten gaat dan zo:
1/x=1/2
x=2
3.
Er is ook een meer algebraische benadering mogelijk die in alle gevallen tot het juiste antwoord zou moeten leiden. Zo'n oplossing kan je ook vinden op Re: Oplossen van een ongelijkheid.
In dit geval is dat misschien wel een beetje overdreven, maar het geeft misschien wel inzicht in de methode, zullen we maar zeggen.
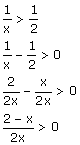
Dan maak je een tekenverloop van de teller en de noemer en 'bedenk' waar de ongelijkheid groter is dan nul.
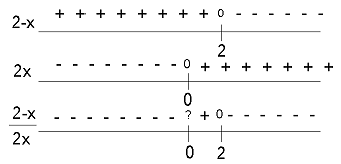
Antwoord: 0 x x 2 2
Kortom: er zijn vele wegen die naar Rome leiden.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 20 januari 2010
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|









 ... x$>$.. of ..
... x$>$.. of ..