WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Voorwaardelijke kans

Ik ben nu al een tijd bezig met een vraag, en ik kom er niet uit! Wie kan me hierbij helpen? Alvast bedankt

Laat gegeven zijn dat 80 procent van een groep studenten dom is en 40 procent rijk. Van de domme studenten haalt 20 procent het beruchte tentamen IOR, en van de rijke studenten 30 procent. De docent, die het hart op de juiste plaats heeft, zorgt er bij zijn correctie altijd voor dat het slagingspercentage van de slimme arme studenten drie keer zo hoog is als dat van de domme rijke studenten. Van de rijke studenten blijkt 70 procent dom te zijn. Van de domme rijke studenten heeft 75 procent een onvoldoende gehaald.

De bekende student Jan slaagt voor het tentamen. Wat is de kans dat Jan arm en dom is?
Yousra
Student universiteit - vrijdag 18 december 2009

Antwoord

Dag mevrouw Yousra,
Noem rijk+dom=rd; rijk+slim=rs; arm+dom=ad en arm+slim=as.
Bepaal eerst deze vier variabelen in procenten van alle studenten:
totaal=rd+ad+rs+as=100;
dom=rd+ad=80;
rijk=rd+rs=40;
rd=0,7(rd+rs)=28;
Dat zijn vier vergelijkingen met vier onbekenden die je kan oplossen.

Vervolgens bekijk je de geslaagden, ook vier onbekenden
(weer in procenten van alle studenten):
Noem ze rd+, ad+, rs+ en as+.
(rd+)+(ad+)=0,2(rd+ad)=16
(rd+)+(rs+)=0,3(rs+rd)=12
Van rd heeft 75% een onvoldoende gehaald, dus 25% is geslaagd:
rd+=0,25*rd;
Het slagingspercentage van as is drie keer zo hoog, dus 75%:
as+=0,75*as
Ook deze vier variabelen kan je nu berekenen.

Ik kom zo op 27 geslaagde studenten, waarvan er 9 arm en dom zijn.
Dus de kans dat Jan arm en dom is 1/3.

Je kan het probleem misschien nog makkelijker oplossen door alle gegevens in een tabel van 3 bij 3 in te vullen.
Ik heb vast een beginnetje gemaakt:

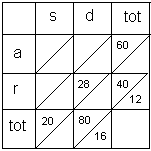
Boven de schuine strepen staan de percentages van het aantal studenten en onder de schuine strepen de percentages (van het totaal aantal studenten) geslaagden in die groep.
Succes,
Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 20 december 2009