|
|
|
\require{AMSmath}



Combinaties uitrekenen en vaststellen met identieke elementen
Stel ik heb een set met n elementen, waarbij identieke elementen ook voorkomen.
bijv S = {A,A,A,A,A,B,B,B,C,C} (10 elementen)
Hoe kan ik nu uitrekenen hoeveel combinaties hiermee te vormen zijn (bestaande uit k elementen) waarbij de volgorde NIET belangrijk is en het ZONDER terugleggen is?
Combinaties uitrekenen voldoet namelijk niet aangezien in deze situatie identieke elementen ook aan de orde komen.
Wat is de algemene manier om bij een soortgelijke samenstelling met een willekeurige set S het aantal mogelijkheden te bepalen?
En daarnaast ook nog die elementen systematisch uit te zoeken bij een variabele waarde van k (algoritme)?
Als iemand in staat is op me punt 1 uit te leggen kan ik zelf al verder uit de voeten.
Sander
Docent - zondag 13 december 2009
Antwoord
Dag Sander,
Ik weet niet of er een standaard algoritme voor bekend is, bij mij in elk geval niet. Na wat puzzelen kwam ik tot de volgende oplossing:
Bovengenoemd voorbeeld met k=8:
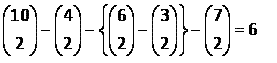
Als er geen beperkingen zijn, dus het aantal A's, B's en C's is onbeperkt, dan gaat het om het aantal herhalingcombinaties van 8 elementen in 3 kleuren: 10 boven 2. (of 10 boven 8)=45.
Dan hebben we er echter te veel:
a=maximaal aantal A's, b=maximaal aantal B's en c=maximaal aantal C's. (hier 5,3 en 2).
Als we te veel A's hebben zijn dat er minimaal a+1=6. Dan blijven er nog 8-6=2 keuze mogelijkheden over:=aantal herhalingscombinaties van 2 elementen in 3 kleuren: 4 boven 2= 6 te veel.
Resteert: 45-6=39.
Met te veel B's blijven er 8-(3+1)=4 over:
aantal herhalingscombinaties van 4 elementen in drie keluren=6 boven 2=15.
Echter als we er 15 aftrekken is dat te veel:
We hebben 8-4=4 keuzemogelijkheden over en daarbij zouden te veel C's kunnen voorkomen, omdat 4 c+1. c+1.
Daarom moeten we van die 15 weer 4-(c+1)+2 boven 2=3 aftrekken.
(=aantal herhalingscombinaties van 4-3 elementen in 3 kleuren)
Resteert: 39-15+3=27.
Tenslotte mogen we niet 3 of meer C's hebben. Er blijven dan nog 8-3=5 keuzemogelijkheden over. Dat is het aantal herhalingscombinaties van 5 elementen in drie kleuren: 7 boven 2=21.
Blijft over: 27-21=6 combinaties.
In het algemeen: Trek k elementen uit m kleuren en maximale aantallen ai:
Begin met k+m-1 boven k (of k+m-1 boven m-1) .
Verminder dit met k-ai+m-2 boven m-1.
Voor alle aj (j i) waarbij aj i) waarbij aj k-(ai+1)moeten we er k-(ai+1)-(aj+1)+(m-1) boven m-1 bij tellen: k-(ai+1)moeten we er k-(ai+1)-(aj+1)+(m-1) boven m-1 bij tellen:
Of: k-ai-aj-3+m boven m-1.
Voorbeeld: k=10,m=3,a1=5, a2=3 en a3=2:
12 boven 2 - (6 boven 2 - 2 boven 2 - 3 boven 2) - (8 boven 2- 5 boven 2)-9 boven 2=1
Inderdaad als we alle 10 knikkers trekken is er maar 1 combinatie mogelijk.
Ik hoop dat dit relaas duidelijk is.
Zo niet hoor ik het wel.
Groeten,
Lieke.
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 15 december 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








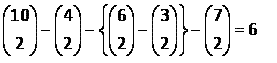
 c+1.
c+1. k-(ai+1)moeten we er k-(ai+1)-(aj+1)+(m-1) boven m-1 bij tellen:
k-(ai+1)moeten we er k-(ai+1)-(aj+1)+(m-1) boven m-1 bij tellen: