|
|
|
\require{AMSmath}



Oppervlakte en integraal
De volgende krijg ik wel opgelost zonder te integreren, maar het is de bedoeling dat ik de vraag oplos d.m.v integreren. Helaas is dit niet erg duidelijk uitgelegd in het boek, dus hopelijk kan iemand mij uitleggen hoe ik deze vraag oplos.
Bepaal de oppervlakte van het gebied, ingesloten door de grafiek van de functies f(x)=2x-1 en g(x)=-2x+2 en de x-as.
Ik heb al de primitieve van de functies uitgerekend, nl F(x)=x2-x en G(x)=-x+2x
Maar hoe moet ik dan verder?
Charlo
Student hbo - donderdag 10 december 2009
Antwoord
Een tekening:
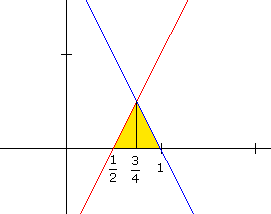
De oppervlakte van de gele driehoek zul je dan in twee stukken moeten verdelen. Een stuk van x=1/2..3/4 en een stuk van x=3/4..1.
$
\eqalign{
& {\rm{Opp}} = \int\limits_{{1 \over 2}}^{{3 \over 4}} {2x - 1\,dx + \int\limits_{{3 \over 4}}^1 { - 2x + 2\,dx} } \cr
& {\rm{Opp}} = \left[ {x^2 - x} \right]_{{1 \over 2}}^{{3 \over 4}} + \left[ { - x^2 + 2x} \right]_{{3 \over 4}}^1 \cr
& {\rm{Enz}}... \cr}
$
...en dan nog even invullen...
Het kan ook wel in een keer, maar dan zou x moeten schrijven als functies van y en dan integreren van y=0..1/2. Dat kan ook, maar dat zal hier (nog) niet de bedoeling zijn.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 december 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










