WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Regressie met een cirkel

Ik meet de x- en y-coördinaten van een bepaald aantal punten en wens de straal ( middellijn ) te bepalen van de cirkel die het best bij deze punten past, alsmede de standaardafwijking.

Voorlopig doe ik het met behulp van de trigonometrie enerzijds, met behulp van de analytische meetkunde anderzijds. De metode is eigenlijk steeds dezelfde, ik ga ervan uit dat men de cirkel kan bepalen die doorheen 3 punten gaat. Trigonometrisch kan ik enkel de waarde van de diameter bepalen ( sin B / b ), niet de coordinaten van het centrum. Met de analytische meetkunde kan ik het snijpunt van twee middelloodlijnen bepalen op 2 rechten die de punten verbinden , wat me het centrum geeft van 'een' cirkel en kan ik verder de afstand bepalen tot ieder punt en dus een standaardafwijking bepalen. Ik laat mijn PC voor het ogenblik steeds opnieuw random drie punten kiezen en alles uitrekenen. Komt hij tot een betere oplossing dan eerder ( = een kleinere standaardafwijking dan bij een vorige berekening ) dan duidt hij zijn laatste cijfers aan als 'best fitting'.

Probleem is echter dat het aantal groepen van 3 punten zeer snel gigantisch groot wordt ( het worden snel miljoenen mogelijkheden !!! ). Ik tracht bijgevolg een metode te vinden die dadelijk met al de gemeten punten rekening houdt. Ogenschijnlijk is het geen eenvoudige opgave, het afschuimen van internet bracht geen aarde aan de dijk...

Dank bij voorbaat, Karel.
Vanden
Iets anders - maandag 23 december 2002

Antwoord

Mijn eerste gedachte hierbij is dat als je de best passende cirkel probeert te vinden het best mogelijk is dat geen enkel punt op die cirkel ligt, dus is de methode waarbij je drie punten zoekt die de 'minste' afwijking geven geen goede methode.

Ik zou zelf denken dat voor de best passende cirkel geldt dat de som van de afstanden van de punten zo klein mogelijk moet zijn. Als je het middelpunt weet, is dat niet zo moeilijk:

Gegegeven een aantal punten (x,y). Bereken eerste het gemiddelde van de x-coördinaten en het gemiddelde van de y-coördinaten. Dit is het middelpunt M van de gezochte cirkel.

Bereken vervolgens de afstanden van de punten (x,y) tot dit middelpunt. Bereken hiervan het gemiddelde. Dit is de straal r van de gezochte cirkel.

Het idee is dat deze cirkel de 'best passende' cirkel is bij een aantal gegeven punten.

Voorbeeld
We nemen (0,0),(4,0),(4,4) en (0,4). De best passende cirkel is volgens deze methode een cirkel door M(2,2) en met straal Ö8.

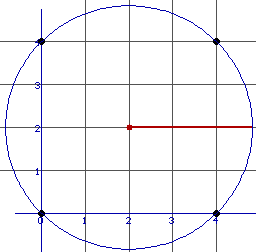
Voorbeeld
Laten we eens de punten (5,0),(4,3),(3,4),(0,5),(-3,4),(-4,3) en (-5,0) nemen. Bovenstaande methode levert (bij benadering):

M(0;2,7) en r4,0

Dit levert:

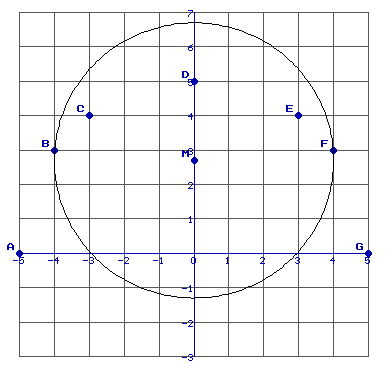
Wel grappig, want hier had natuurlijk ook een cirkel kunnen worden getekend waar ALLE punten op liggen, maar dat is dan misschien weer iets anders? Of juist niet?

De vraag blijft of deze methode de 'best passende' cirkel oplevert (misschien moet je dat eerst definieren!). Het hangt een beetje af van de toepassing die je voor ogen hebt, maar dit is wel weer zo eenvoudig, dat het daarom alleen al het proberen waard is (als je er van uitgaat dat je een redelijk aantal willekeurige punten hebt die zo ongeveer op een cirkel liggen, dan gaat het wel goed...).

Er zijn natuurlijk nog allerlei varianten denkbaar. Zou je bijvoorbeeld ook kunnen kijken naar het gemiddelde van de kwadraten van de afstanden van al die punten tot M? Of moet je kijken naar de horizontale of verticale afstanden? Een eerste stap is precies te formuleren wat we onder een 'best passende' cirkel moeten verstaan. Op basis daarvan kan je dan (denk ik) wel een rekenmodel bedenken die het juiste resultaat oplevert.

Anders gezegd, moet het model bij het tweede voorbeeld zoiets als de gegeven oplossing geven of had je toch liever de cirkel gehad waar alle punten op liggen?

Op onderstaande website kan je een programma downloaden dat dit probleem wel oplost. Bij het tweede voorbeeld krijg je dan inderdaad een cirkel met M(0,0) en r=5.
Title "Fit circle to group of points";
Variable Xp;                    // X coordinate of point
Variable Yp;                    // Y coordinate of point
Parameter Xc;                   // X position of circle center
Parameter Yc;                   // Y position of circle center
Parameter R;                    // Radius of circle
Function sqrt((Xp-Xc)^2 + (Yp-Yc)^2) - R;
Data;
-5	0
-4	3
-3	4
0	5
3	4
4	3
5	0
Maar dan wel in 0,05 seconde...:-), dus hier moet iets op te verzinnen zijn. Dit probleem is nog niet opgelost..., maar misschien kun je nu vast verder. Het gaat er dus om de functie

sqrt((Xp-Xc)^2 + (Yp-Yc)^2) - R te minimaliseren...
Zie Circular Regression

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 25 december 2002