WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Betrouwbaarheid van een getuige

In een bepaalde stad zijn er 2 taxibedrijven. het ene bedrijf heeft groene taxi's, de andere blauwe. In de stad zijn er 85% blauwe en 15% groene taxi's.

Op een nacht raakt een taxi betrokken in een auto-ongeval. de taxi vlucht weg. Een getuige ziet dit gebeuren en zegt dat de taxi groen is. Die getuige heeft een probleem met kleurnonderscheidingsvermogen. in 80% van de gevallen zegt hij de juiste kleur, in 20% van de gevallen vergist hij zich.

De kans dat de taxi inderdaad groen was als de getuigen hem groen noemt is dan 100 taxis = 85 blauwe en 15 groene
van de 15 groene zal hij er 12 groen noemen. Van de 85 blauwe zal hij er 17 groen noemen = 29 groene waarvan 12 juiste = 12/29

Stel nu dat er een tweede getuige komt en die beweert ook dat de taxi groen is, maar de tweede getuige heeft hetzelfde kleurenonderscheidingsprobleem. Om hiervan een kansboom te maken ( met de 2 getuigen ), zit ik in de knoei. Ik zie niet goed in welke takken ik die tweede getuige moet hangen. (en doordat ik mijn kansboom niet heb kan ik ook geen verdere dingen berekenen met 2 getuigen).

Kan u mij op weg helpen met de subvraag: 'is de kans om twee dergelijke getuigenissen te krijgen kleiner dan 5 % als de eigenlijke taxi-kleur blauw is?'

Kan u mij hier een hint geven hoe ik daar moet aan beginnen. Ik weet eigenlijk niet goed hoe of wat ik hier moet berekenen.
jinthe
3de graad ASO - dinsdag 24 november 2009

Antwoord

Wat dacht je hiervan?

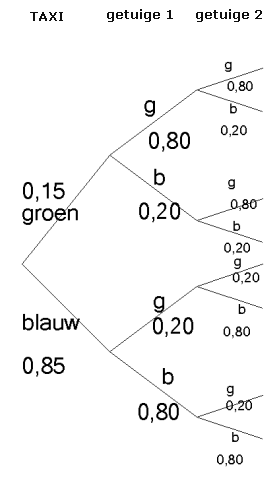
Zou het dan lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 29 november 2009