WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Inversie

Beste mensen,

Het wil mij niet lukken de volgende vraagstukken op te lossen. Graag wil ik gebruikmaken van uw hulp.

VRAGEN:
1)
Gegeven een punt M en cirkels C1 en C2 niet door het punt M Hoe kan ik een cirkel C Construeer door M en orthogonaal met cirkels C1 en C2 .

2)
Gegeven een punt M en cirkels C1 en C2 niet door het punt M Hoe kan ik een cirkel C Construeer door M die cirkels C1 en C2 raakt .

Alvast zeer bedankt
M.Bouk
Student hbo - donderdag 22 oktober 2009

Antwoord

Beste M?
Vraag 1 is geen moeilijke constructie, kan met passer (en lat).
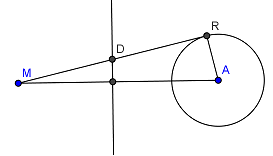
Je ziet hier een van de gegeven cirkels, bijvoorbeeld C1 en het punt M.
Vanuit M is een raaklijn getekend (het raakpunt R is te vinden door een cirkel te tekenen met middellijn MA) .
D is het midden van MR.
Alle cirkels met hun middelpunt op de lijn door D loodrecht op MA die door M gaan staan nu loodrecht op C1.

Je wil dit natuurlijk wel bewijzen, maar daarvoor weet ik niet wat je hebt geleerd over inversie.
Deze constructie voer je nu ook uit voor de tweede cirkel en je krijgt twee lijnen. Het snijpunt is het gevraagde middelpunt.

Wat betreft vraag 2: Een passer en lat constructie is een stuk ingewikkelder.
Met een programma als GeoGebra of Cabri kan het relatief eenvoudig:
De middelpunten van de rakende cirkels liggen nu op een hyperbool.
Zokan je twee hyperbolen tekenen en het snijpunt bepalen.
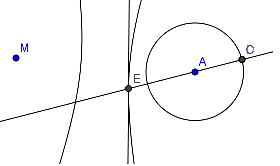
Weer de cirkel C1 en punt M.
Kies een punt D op C1.
Teken de lijn AD en de middelloodlijn van MD. Het snijpunt ligt op de bedoelde hyperbool.
Door nu D langs de cirkel te laten lopen kan je de meetkundige plaats van dat snijpunt tekenen.
Zo ook voor C2 en M.

Met dank aan dk twee mooie constructie mogelijkheden van probleem 2 met passer en lat:
Voor vraag 2 opgelost met passer en lat:
http://www.pandd.demon.nl/raakprob(2).htm#s102
en met inversie zie:
http://www.pandd.demon.nl/raakprob.htm#a102
Beide als deeloplossing van het Raakprobleem van Apollonius.

De site geeft je tevens een prachtige introductie, en verdieping over inversie. Zeer de moeite waard!

Als je nog vragen over die constructie hebt hoor ik het wel.
Groeten,
Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 oktober 2009

Re: Inversie