WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Berekenen van een zijde van een driehoek

Hier een voorstelling van de driehoek:

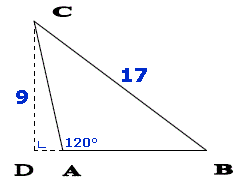
Gegeven zijn:
$\angle$D=90°
CD=9
BC=17
$\angle$A=120°

Wat ik totaal niet snap is hoe ik AC en AB moet berekenen.
Daarnaast moet ik de hoeken ABC en BCA berekenen.

Ik weet wel dat soscastoa gebruikt moet worden voor de hoeken, en misschien de stelling van Pythagoras ?
Ik ben maar pas bezig met goniometrie, hoop dat u mijn vraag kan beantwoorden.
Alvast bedankt.
F
Leerling bovenbouw havo-vwo - zondag 9 augustus 2009

Antwoord

In rechthoekige driehoek DAC weet je dat ÐDAC=60° en DC=9. Daarmee kan je DA en AC berekenen. Met de tangens c.q. de sinus (eventueel ook nog met de 60-30-90-driehoek).
Zie eventueel Rekenen met sinus, cosinus en tangens

AB kan je berekenen als je DA kent want je kent DB immers ook al (stelling van Pythagoras).

Om hoek ABC te berekenen kan je gebruik maken van de tangens in driehoek DBC. Als je hoek ABC en hoek BAC (=120°) kent weet je hoek BCA ook (som van de hoeken).

Hopelijk helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 augustus 2009