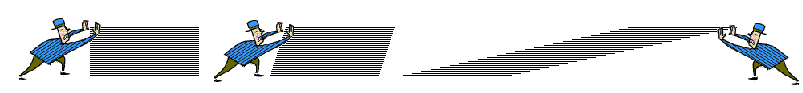|
|
|
\require{AMSmath}



Inhoud berekenen van een afgeknotte excentrische kegel
Hoe bereken ik de inhoud van een afgeknotte excentrische kegel?
Jan Lo
Student hbo - dinsdag 14 juli 2009
Antwoord
Dag Jan,
Je beschrijving is wel erg beknopt, maar net als het feit dat het oppervalk van een driehoek alleen afhankelijk is van de basis en de hoogte geldt dat de inhoud van een kegel niet afhankelijk is van de plaats van de top.
Als je je voorstelt dat een kegel is gemaakt door allemaal dunne schijfjes op elkaar te stapelen (de schijfjes worden uiteraard steeds kleiner naarmate je dichter bij de top komt) kan je je voorstellen dat de inhoud niet verandert als je die stapel schijfjes een beetje scheef duwt.
Vergelijk het maar met dit plaatje waar een rechthoek scheef wordt geduwd zodat een parallellogram ontstaat. Het oppervlak blijft net zo groot als de oorspronkelijk rechthoek!
Als dit je vraag niet helpt oplossen hoor ik het wel, maar dan met wat meer concrete gegevens hoop ik .
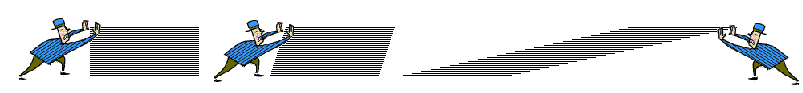
Succes,
Lieke.
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 juli 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|