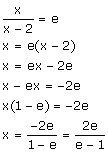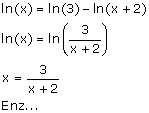WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vergelijking met meerdere logaritmen

Ik vraag me het volgende af, ik moet van de volgende vergelijking aangeven wat de waarde voor x is:

ln x = 1 + ln (x-2)

Ik weet dat je met de regels voor logaritmen zou mogen zeggen dat:
ln x - ln (x-2) = 1 en volgens mij ook:
ln (x/(x-2)) = 1

Als dit klopt zou:
x/(x-2) = e¹

Klopt dit, en hoe moet ik nu verder, want ik weet niet wat ik verder nog kan doen. Een tweede vergelijking van deze opdracht is bijvoorbeeld ln x = ln 3 - ln (x+2)
Zijn er niet standaardregels om met ln (x+/-a) om te gaan? ik kon ze niet vinden bij de rekenregels voor logaritmen...
anonie
Leerling bovenbouw havo-vwo - zondag 21 juni 2009

Antwoord

Volgens mij gaat het heel goed en heb je verder geen 'rekenregels' meer nodig. Als je bij x/(x-2)=e bent aangekomen kan je de vergelijking verder op gaan lossen.

Dus gewoon even doorbijten...

Bij de tweede vergelijking doe je hetzelfde:

Probeer het!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 juni 2009