WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Breukspitsen met een 3e macht

De volgende opgaven bezorgen nogal wat hoofdbrekens:
1) f(x)=1/{x³(x+1)} Ik had dat als volgt gedacht:
A/x³ + B/x + C/(x+1). Omdat dan A=1, C=-1 en B=0 uitkomen, denk ik dat het niet goed is.

2) f(x)=(x-4)/(x+1)³= Het leerboek adviseert noem (x+1)=u
en dan is x=u-5. Opgave wordt dan (u-9)/u³.Ik heb uitgewerkt als volgt: (u-9)/u(u²)= A/u + B/u² enz.
De uitkomst wordt dan f(x)= -5/(x+1) + 1/(x+1)²

Wie kan beoordelen of dit goed gedaan is? Bij voorbaat veel dank!
Johan
Student hbo - donderdag 11 juni 2009

Antwoord

dag Johan,

De eerste opgave is niet correct.
Er ontbreekt nog een term D/x²
Omdat de noemer hier van de graad 4 is, heb je ook 4 parameters nodig voor de splitsing.
De tweede opgave is ook niet juist.
Als x+1 gelijk is aan u, dan is x toch gelijk aan u-1?? Waarom die 5?
Vervolgens kun je zonder parameters direct de breuk uitwerken:

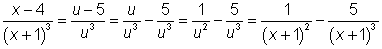
groet

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 12 juni 2009

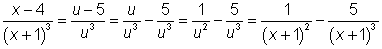
Re: Breukspitsen met een 3e macht