WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Twee kruisjes in negen hokjes

Ik snap het volgende niet: wanneer er 9 hokjes (zoals bij boter-kaas-en-eieren) zijn en er worden 2 kruisjes ingezet die elkaar NIET mogen raken in een rij of kolom, de volgorde is NIET van belang, hoeveel mogelijkheden zijn er dan?

Ik dacht zelf aan 9 nCr 2 =36.
Maar de uitwerkingen zeggen: ¹/₂·9·4=18

Wie kan mij helpen, en waar komt die ¹/₂ vandaan?
Bram
Leerling bovenbouw havo-vwo - vrijdag 15 mei 2009

Antwoord

Die 9 uit 2 zijn alle combinaties van 2 kruisjes bij 9 hokjes. Dat kan het niet zijn want daar zitten dan zeker een aantal 'foute' mogelijkheden bij.

Verder hangt het er (m.i.) nog van af of 'raken in de hoekpunten' nu wel of niet mag.

Hoekpunten raken mag
Ik ben maar 's gewoon gaan tellen:

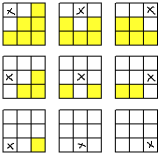
Ik kom dan uit op 24 mogelijke combinaties.

Hoekpunten raken mag niet
Tellen maar weer:

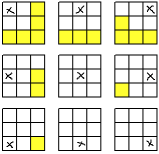
Ik kom dat uit op 16 mogelijke combinaties.

In beide gevallen kom ik niet uit op 18. Ik begrijp ook niet helemaal wat de redenering achter die 18 zou moeten zijn.

Maar ik zit de hele dag al te klunzen, dus wat denk jij? Zit ik goed? Zou de gegeven uitwerking gewoon niet kloppen? 't Zou zomaar kunnen. Zeg jij 't maar!

naschrift

Achteraf heeft svr bedacht dat als met 'niet raken' bedoeld wordt dat er niet twee kruisjes in eenzelfde rij of eenzelfde kolom getekend mogen worden de gegeven oplossing wel klopt.

De eenvoudige redenering is dan als volgt: je begint met 9 mogelijkheden voor je eerste kruisje. Aangezien je tweede kruisje niet in dezelfde rij/kolom mag staan, heb je voor je tweede kruisje nog maar 4 plaatsjes over.
Dat geeft dus een totaal van 9.4=36 mogelijkheden.

Natuurlijk wordt op deze manier twee maal een zelfde "koppel" kruisjes getekend. Vandaar dat je de dubbele mogelijkheden eruit moet halen door te delen door twee.

Mooi!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 16 mei 2009