WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

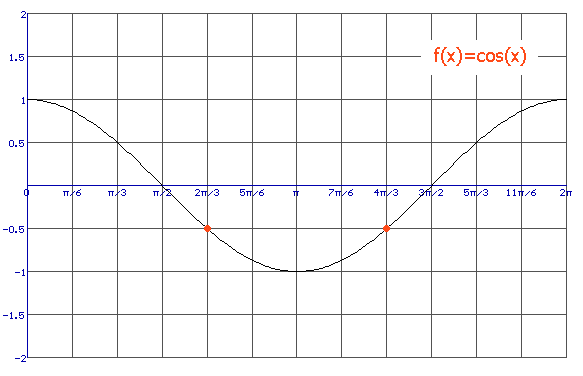
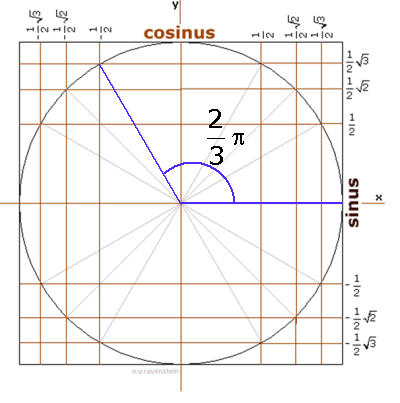
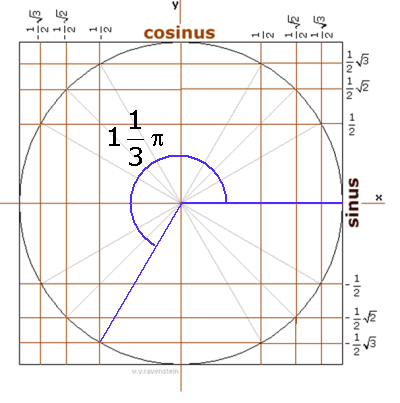
Goniometrische vergelijking oplossen

Hallo. ik zit in 5vwo en ben bezig met goniometrische vergelijkingen oplossen, maar ik loop tegen iets aan wat ik niet snap.
De opdracht is dit:
Bereken exact de oplossingen van -cos(2x) = ¹/₂ op [0,2p]
Ik zie dan: cos(2x) = -1/2 maar ik kom niet echt verder... Volgens het antwoordenboek: 2x = 2/3p+k·2p
Kunnen jullie uitleggen hoe deze stap in elkaar zit? Ik ben er vrij zeker van dat het dan wel weer lukt ;-)
Mirjam
Leerling bovenbouw havo-vwo - donderdag 14 mei 2009

Antwoord

Na cos(2x)=-¹/₂ moet je je gaan afvragen welk waarde hoort er bij cos(...)=-¹/₂. Dat kan je doen met een grafiek van cosinus:

Je ziet dat tussen 0 en 2p er twee hoeken zijn die voldoen.

Je kunt ook gebruik maken van de eenheidscirkel:

Dit is natuurlijk hetzelfde! Dus je krijgt dan:

cos(2x)=-¹/₂
2x=²/₃p+k·2p of 2x=1¹/₃p+k·2p
...

Zou het dan verder lukken? Je moet nog wel even verder rekenen en houd er rekening mee dat x moet liggen tussen 0 en 2p.

We horen het wel...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 mei 2009