WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Snijpunt berekenen

Ik ben programmeur, al een tijdje van school en kom maar niet uit het volgende probleem dat ik tegenkom als onderdeel van een simulator programma dat ik aan het schrijven ben:

Neem aan dat a en b tanks zijn. Tank b beweegt in de richting van de vector met snelheid Vb onder hoek a. Tank a staat stil. Tank a en b zijn verwijderd van elkaar over een afstand s.

Op t=0 wil tank a op tank b schieten. De kogel heeft een snelheid Vkogel. Om b te kunnen raken zal a moeten anticiperen op de snelheid en richting van b en zal moeten schieten onder hoek beta.

Op t=0 is het kanon exact op b gericht. Het kanon kan in elke richting 360 graden draaien met hoeksnelheid h. A lost het schot op t=1. Om b te kunnen raken op t=2, moet a niet alleen anticiperen op Vb, maar ook op de tijd die het kost om het kanon te draaien in de richting van snijpunt x.

Gegeven op t=0: coordinaten van a en b, snelheden Vb en Vkogel, alsook hoek alpha, hoeksnelheid h en afstand s.
Bepaal het tijdstip t=1 waarop moet worden geschoten geef de waarde van hoek b op dat moment.

Ik heb de situatie getekend:

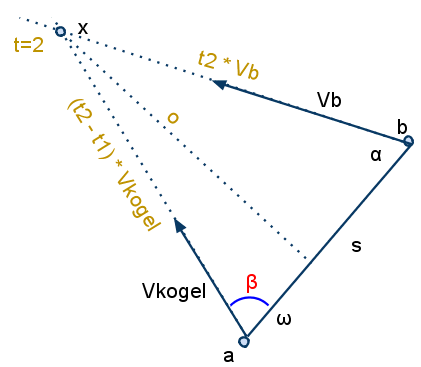
Mijn halve oplossing tot nu toe:

(1) o = t₂ · Vb · sin(a)
(2) o = (t₂ - t₁) · Vkogel · sin(b)
(3) b = h · t₁

en dus:

(4) sin(b) = (t₂ · Vb sin(a)) / (t₂ - t₁) · Vkogel

Echter, hoe werk ik t₂ weg, zodat ik b als functie van t₁ kan schrijven? Ik kan t₂ schrijven als:

(5) t₂ = (-t₁ · Vkogel · sin(a)) / (Vb · sin(a) - Vkogel · sin(b))

Maar als ik (5) invul in (4), explodeert de boel een beetje en krijg ik het niet meer vereenvoudigd tot:

t₁ = ...iets met alleen maar bekenden...
Erik v
Iets anders - zondag 10 mei 2009

Antwoord

Hallo, Erik.

In uw vraagstelling schrijft u t=1 en t=2 ipv t₁, t₂; dit is natuurlijk niet juist; in uw halve oplossing doet u dat niet meer, dat is okee.

Als u de lijn van A naar B als x-as neemt, en de lijn door A loodrecht daarop als y-as, dan gebruikt u van het snijpunt van de kogelbaan en de baan van tank b alleen de y-coördinaat, en vergeet de x-coördinaat.

Gebruikt men ze allebei, dan krijgt men TWEE vergelijkingen met de twee onbekenden t₁ en t₂, namelijk: (ik gebruik een n ipv een èta)

(t₂-t₁) v_kogel cos (n t₁) = s - t₂ v_b cos(a)
(t₂-t₁) v_kogel sin (n t₁) = t₂ v_b sin(a).

Deze twee vergelijkingen zijn weliswaar niet lineair, maar men kan ze toch (benaderend) oplossen, als volgt:

Vermenigvuldig de eerste vergelijking met sin(a), de tweede met cos(a), en tel daarna beide vergelijkingen bij elkaar op. Gebruik makend van een bekende goniometrieregel krijgt men dan:

t₂ = t₁ + (s sin(a))/(v_kogel sin(n t₁+a).

Substitueert men dit in de eerste vergelijking, dan krijgt men een vergelijking waar als onbekende alleen t₁ in voorkomt.
Deze kan men vereenvoudigen, en, bij gegeven waarden van de parameters a, n, v_b, v_kogel en s, met behulp van een rekenmachine met 'trial and error' benaderend oplossen.
Zodra u t₁ hebt, vindt u mbv de laatste hierboven opgestelde vergelijking ook t₂.
(Het geval a = p/2 moet u enigszins afwijkend oplossen.)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 mei 2009