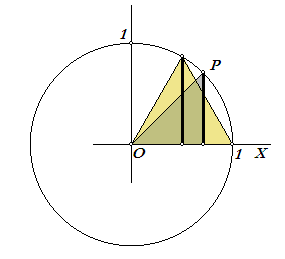WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Speciale hoeken op de goniometrische cirkel

Dit is een reactie op vraag 58994

Bedankt, maar ik heb de vraag niet duidelijk genoeg gesteld denk ik. Het is eerder de bedoeling om via de goniometrische cirkel de waarden te kunnen afleiden van sinus, cosinus en tangens van 0, pi/6, pi/4, pi/4, pi/2, pi en 3pi/2. Ik denk dat er een bepaalde invalshoek is om naar de cirkel te kijken, maar ik ben er nog niet echt achter welke deze is..

Nogmaals bedankt bij voorbaat en sorry
Annelies
Anneli
Student universiteit - dinsdag 14 april 2009

Antwoord

Dag Annelies,

Als je sinus van pi/6 kan vinden in een driehoek, dan kan je die voor pi/3 in dezelfde driehoek vinden (driehoek ADC, in het vorige antwoord).
En als je dan ook probeert een dergelijke driehoek te tekenen (te passen) in de goniometrische cirkel...
En dat kan je natuurlijk ook doen voor een rechthoekige driehoek waarvan een hoek gelijk is aan pi/4.
En bedenk dan dat de sinus gelijk is aan de van teken voorziene afstand van een punt P op de cirkel tot de y-as (x-coördinaat) en de cosinus de afstand tot de x-as (y-coördinaat).
P bepaalt dan de hoek (POX; zie het plaatje).
Voor hoeken als pi/2, pi en 3pi/2 kan je direct de gewenste coördinaat 'zien' in het assenstelsel.

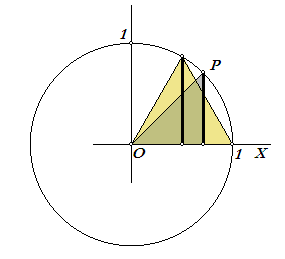
Nb. De straal van de goniometrische cirkel is gelijk aan 1.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 april 2009