WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gemiddelde en variantie uniforme verdeling

Een vakantieganger wil een dagje naar een in de buurt gelegen oud stadje. Hij weet niet wanneer de stoptrein in het dorpje waar hij logeert vertrekt naar die plaats. Daarom loopt hij maar op goed geluk naar het treinstation. Daar vertrekt stipt op tijd elk uur een trein naar de stad. De tijd dat de vakantieganger moet wachten op de binnenkomst van de trein is een stochast X.

b. Geef het voorschrift van de bijbehorende kansdichtheidsfunctie.

in het antw.boek staat dat dat moet zijn:

f(X)= X/60 als 0X60
f(X)= 0 als X0 of X60

maar in het informatieboek staat dat het moet zijn:

f(X)= 1/60 als 0X60
f(X)= 0 als X0 of X60

ik denk zelf dat het de laatste moet zijn en mijn leraar ook. en als je de verwachting gaat berekenen blijkt ook dat het antwoord overeenkomt met de onderste versie. Maar waarom schrijven ze dan de bovenste op in het antw.boek. Is hier misschien een regel voor dat deze antw eigenlijk het zelfde betekenen ofzoiets?
kunnen jullie mij vertellen hoe het nou wel goed is en waarom dat zo is?

c. Bereken E(X) en Var(X)

E(X) is 30
als ik Var(X) uitreken met Y1=(X-30)².(1/60)

dan krijg ik eruit Var(X)=300 terwijl het antwoord volgens het antwoordenboek Var(X)=9000 moet zijn!!

wat doe ik fout en hoe moet je dit dan wel uitrekenen?

alvast heel erg bedankt voor het beantwoorden!!

groetjes van anne
anne z
Leerling bovenbouw havo-vwo - dinsdag 10 december 2002

Antwoord

In dit geval heeft het informatieboek gelijk. Omdat het hier over een continue variabele gaat en met het gegeven dat alle tijden even waarschijnlijk zijn kan je dit vertalen in een continue stochastische variabele die constant is op het interval [0,60].

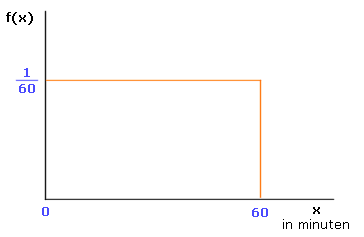
De hoogte van de rechthoek in bovenstaande grafiek volgt uit het gegeven dat de oppervlakte onder de curve gelijk aan 1 moet zijn. Met een 'lengte' van 60 wordt de hoogte dus ¹/₆₀. Anders geformuleerd:
f(x)=¹/₆₀ (0x60)
f(x)=0 (elders)

E[x]=₀ò⁶⁰x·f(x)dx
E[x]=₀ò⁶⁰x·¹/₆₀dx
E[x]=[¹/₁₂₀x²]⁶⁰₀=30

Var[x]=₀ò⁶⁰(x-E[x])²·f(x)dx
Var[x]=₀ò⁶⁰(x-30)²·¹/₆₀dx
Var[x]=[(x-30)³/180]⁶⁰₀=300

Dus jij had het helemaal goed...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 10 december 2002