WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Negatief van een implicatie opnieuw een implicatie?

Hallo,

Een voorbeeldoplossing bij een bepaalde oefening van verzamelingenleer meldt dat ¬(P = Q) equivalent is met P = ¬Q

(of in woorden: negatief van P impliceert Q is equivalent met P impliceert niet-Q)

Ik vraag me af of/hoe dit mogelijk is. Het negatief van een implicatie kan toch niet opnieuw een implicatie zijn? Moet de oplossing niet gewoon P ^ ¬Q zijn? (of in woorden: P en niet-Q)

De precieze opgave:
¬(∀n ∈ : n² 10 = n 5) is equivalent met...
Voorbeeldoplossing: ∃n ∈ : n² 10 = n 5
Mijn oplossing: ∃n ∈ : n² 10 ^ n 5
Kelly
Student universiteit België - zondag 25 januari 2009

Antwoord

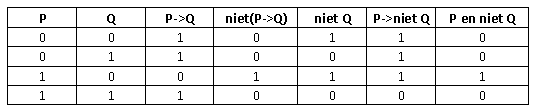
Je conclusie dat $\neg$(P$\Rightarrow$Q) equivalent zou moeten zijn met P$\Rightarrow\neg$Q is te voorbarig. Dat is niet juist inderdaad. Overigens $\neg$(P$\Rightarrow$Q) en P$\wedge\neg$Q klopt wel...

Als niet geldt dat 'voor alle n volgt B' dan kan er een n zijn zonder dat daar B uit volgt, sterker waaruit dan dus zelfs niet B volgt. Dat hoeft niet altijd maar er is mogelijk een waarde voor n waarvoor dat geldt.

Nog anders geformuleerd: 'normaal' gesproken volgt uit n²$>$10 dat n$\geq$5.
Als dat niet waar is dan is er dus een n waarvoor geldt dat n²$>$10 waar uit volgt dat n$<$5.

Hopelijk helpt dat...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 januari 2009