WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een recursieve formule om het verloop van een epidemie te voorspellen

Ik zit met het volgende vraagstuk, en ik geef hier alleen de belangrijkste gegevens. Er is een epidimie. In het begin zijn er 10 mensen ziek, op een bevolking van 10 000 mensen, ze hebben elk 50 contacten per dag en van deze 50 wordt er 5% ziek. Nu moet ik een tabel zien te krijgen bij deze gegevens. Daarom moet ik een kloppende formule opstellen. Zelf heb ik dit al bedacht (maar dit klopt niet echt) :

U (n) = U (n-1) * 50/ 10 000 - U(n-1) * 0.05 + U (n-1)
n = {10}

Waarschijnlijk is er niemand die ziet hoe ik hier nou weer bij kom en daarom zal ik even een soort van uitleg proberen te geven.
Voor het = teken U (n) Het aantal zieken op dag U.
Vervolgens U (n-1) wat dus het aantal zieken op dat moment is.
Keer 50 contacten op een dag, maar van die 50 contacten is een deel al ziek, en zodoende moet ik volgens mij de kans berekenen dat een zieke in contact komt met een gezond persoon,. Vandaar dat ik 10 000 - U (n-1) doe, de totale bevolking min het aantal zieken dat er al is. Volgens mij doe ik hier iets fout, maar ik zou niet weten wat.
Dan keer 0.05 (de 5% die ziek wordt dus)
Plus het aantal zieken dat er al was die dag.

Alvast bedankt!
Marja
Leerling bovenbouw havo-vwo - donderdag 16 oktober 2008

Antwoord

Volgens mij 'zegt' het 'model' alleen maar dat elke zieke 5% van de 50 contacten aansteekt. Dat verandert (kennelijk) niet als er meer of minder ziek dan wel gezond zijn...

Dat is natuurlijk wel een raar model maar uit de beschrijving kan ik er niets anders van maken.

U(0)=10
U(1)=10+10·50·0,05=10+10·2,5=10·3,5=35
U(2)=35·3,5=122,5
U(3)=122,5·3,5=428,75
...
U(n)=U(n-1)·3,5

Dus dat gaat lekker zo...

Een tabel? Kan ook:

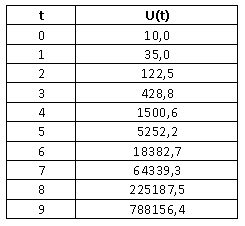
Maar je voelt wel aan, dat kan helemaal niet. Er zijn maar 10.000 mensen, dus na 5/6 dagen is iedereen ziek. Dat is niet zo gek. Het is tenslotte een epidemie...

Ik geef toe dat het model waarschijnlijk niet erg realistisch is, maar ja dat kan je wel 's hebben met modellen.

Maar misschien valt het ook wel mee. 't Is een behoorlijk snel om zich heen grijpende ziekte, dus is die voorspeling van 5/6 dagen misschien niet eens zo gek nog niet...

Meer kan ik er ook niet van maken...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 19 oktober 2008