WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte van een vierkant met vierkanten

Ik wil de oppervlakte van een groot vierkant uitzoeken. In dat vierkant staan 2 vierkanten waarvan de oppervlaktes gegeven zijn, 1 ervan staat echter schuin op gegeven en 1 in de hoek die tegen de zijde van de middelste vierkant ligt.
In de hoeken van het vierkant staan dan 4 gelijke driehoeken (1 met een klein vierkant erin).
Ik kan er niet op komen hoe ik aan de lengtes van de zijden kan komen om zo tot de totale oppervlakte te komen. Alleen van de 2 binnenste vierkanten kan ik de lengtes van de vierkanten vinden maar kan geen manier vinden om daarmee door te kunnen rekenen.
rob
Leerling bovenbouw havo-vwo - woensdag 27 november 2002

Antwoord

Hoi,

Dit is de figuur die erbij hoort. Ik heb een aantal maten toegevoegd. Aangezien het om vierkanten gaat, kan je uit hun oppervlakte de lengte van de zijden berekenen met S=z².

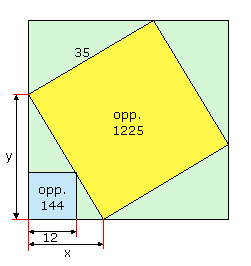
Bemerk dat de 4 driehoekjes rond het vierkant met oppervlakte 1225 congruent zijn en dus dezelfde oppervlakte hebben. De oppervlakte van het grote vierkant is dus 1225+4.(x.y/2)=1225+2xy.

We moeten dus enkel nog x en y berekenen. Dit lijkt op het ladderprobleem (een ladder van een zekere lengte staat tegen de muur en er staat een vierkante doos onder met gekende afmetingen).

Concreet hebben we:
x²+y²=35²
12/x+12/y=1 (rechte door (x,0) en (0,y) moet (12,12) bevatten)

Hieruit halen we:
(x+y)²-2xy-35²=0
xy=12(x+y)

en dus met z=x+y:
z²-24z-1225=0
waaruit z=(24+74)/2=49 of z=(24-74)/2=-25
z moet positief zijn aangezien het een som van lengtes is. Dus: x+y=49 en xy=12.49=588
x en y zijn dus de oplossingen van t²-49t+588=0.
Zodat: x=(49+7)/2=28 en y=(49-7)/2=21 (of omgekeerd)

De gezochte oppervlakte is dus 1225+2.28.21=2401

Heel mooie, vooral omdat het gehele oplossingen heeft...

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 29 november 2002