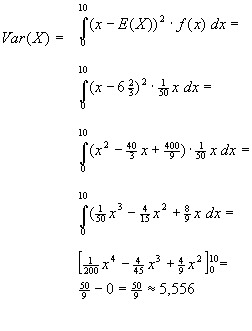WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kansdichtheidsfuntie en verwachtingswaarde

gegeven is de continue stochast met de kansdichtheidsfunctie:

f(X)= x/a als 0X10
0 als X0 of X10

ik heb al berekend dat a 50 moet zijn, zodat de opp onder de grafiek 1 is.

dan krijg je de opdr:
Bereken nu de volgende kansen:
P(0X3)
P(2X8)
P(X5)

Nou dan ga je dat berekenen. bv de eerste wordt, als ik naar het antw. in het boek kijk gewoon zo berekend:
¹/₂.3.3/50=9/100

WAT IK HIERAAN NIET BEGRIJP:
ik zou denken dat je dit op deze manier zou berekenen al gevraagd werd: P(0X3)
Hoe kan je in je berekening het verschil mkn tussen de kans gevraagd in de opgave en de kans die ik hierboven heb staan?

Daarna wordt gevraagd:

Bepaal de verwachting E(X) en de variantie Var(X).

Eerst probeerde ik dit op te lossen op een makkelijke manier met mijn gr (TI83), nl:
seq(x,x,0,10)sto L1
seq(x/50,x,0,10)sto L2

1-Var Stats

maar hier komen allemaal verkeerde antw uit. Hoe kan dat, en is er een andere hele simpele manier om dit met je gr te berekenen?

toen ben ik het gaan berekenen met de regels en integralen.

E(X) lukt me om op deze manier goed te berekenen. maar bij var(X) gaat het denk ik een beetje mis met het integreren, want als ik de integraal bij Y1 in mijn gr zet en dan calc/7 doe dan krijg ik wel het goede antw.
dus nu zou ik graag willen weten wat ik fout doe, ik doe:

10 10
Var(X)=S(X-20/3)².X.1/50=[1/3(X-20/3)³.1/100X²]=
0 0
(1/3(10-20/3)³.1/100.10²)-0= 12,35

maar dat is dus het foute antw. het zou 50/9=5,56 moeten zijn, dat krijg ik er ook uit met mijn gr. dus wat doe ik fout als ik het op de hand bereken?

alvast heel erg bedankt voor het beantwoorden!!
anne z
Leerling bovenbouw havo-vwo - dinsdag 26 november 2002

Antwoord

Je eerste vraag:
Zoals je al schreef keek je naar een continue kansverdeling.
Dat betekent dat elk getal tussen 0 en 10 als uitkomst van je kansexperiment kan voorkomen. Als elk getal kan voorkomen, betekent dat er oneindig veel mogelijke uitkomsten zijn en dus dat de kans dat een voorafgekozen waarde als uitkomst komt oneindig klein is (ofwel gelijk is aan 0).
Dus P(X=3) = 0, want dat je uitkomst precies 3 is en niet bijvoorbeeld 2,9999999 of 3,00001 of 3,001 of .... is oneindig klein.
In feite kijk je naar de oppervlakte boven X = 3, maar boven X = 3 ligt alleen maar een lijntje en dit heeft geen oppervlakte.
Conclusie: P(0X3)=P(0X3), want de grenzen doen er niet toe.

Je tweede vraag:
Bij de eerste manier waarop de verwachtingswaarde probeerde uit te rekenen, heb je van je continue verdeling ineens een discrete verdeling gemaakt. Je doet plotseling alsof het een histogram is, in plaats van een lijn (zie plaatje hieronder).

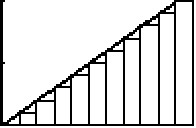
Je tweede manier met behulp van integreren is dus de juiste.
Wanneer je de variantie handmatig gaat integreren leidt dit tot het volgende:

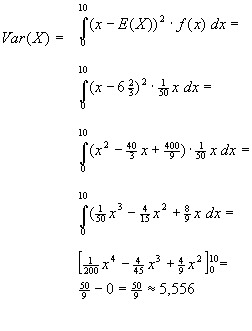
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 27 november 2002