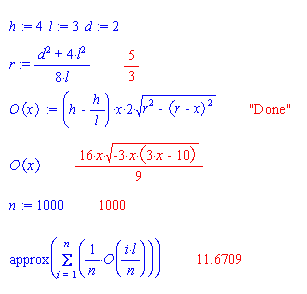WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Afgeknotte cilinder

Met de afgeleide formule van 17-11-2001(RJ Timmermans) krijg ik niet het juiste Volume als antwoord.
Het volume uit het voorbeeld moet minder zijn dan: 0.5 r²xh, als r=5/3 en d=2 dan is V17,45
V=17,45 is het volume van de wig, die over blijft, als de cilinder zodanig wordt afgesneden, dat het grondvlak nog juist een cirkel is.

Is de afleiding met Inter Active wel goed?

Zelf reken ik met de formule uit Vademecum van de Wiskunde van Otto Teller.

Henk

henk
Iets anders - donderdag 21 november 2002

Antwoord

Erger nog, mijn integraal deugt niet.
Ik zit er een factor l naast.
Ik zal moeten uitzoeken hoe het nu precies zit, maar wanneer ik het voorbeeld numeriek doorreken krijg ik een inhoud die een derde is van wat ik met de integraal had berekend:

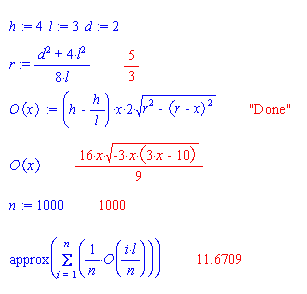
Ik heb er nog wat verder mee zitten spelen en het blijkt steeds een factor l te schelen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 25 november 2002