WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte bolkap

Een waarnemer, die zich op een hoogte h boven het bolvormig veronderstelde aardoppervlak bevindt, ziet een deel van onze planeet. Druk de oppervlakte van deze waarneembare bolkap uit als functie van de aardstraal r en h.

Ik heb dit probleem opgelost, maar men zegt dat dit niet wiskundig kan bewezen worden. De oplossing klopt echter wel, zowel algemeen als met een concreet voorbeeld. Ik maak géén gebruik van congruente driehoeken.

Ik redeneer als volgt:
ik teken een cirkel met straal r, x noem ik de hoogte van de bolkap. Daarop teken ik een cirkel met straal r+h, h is de hoogte boven het bolvormig aardoppervlak.
Nu stel ik :
h/(h+r)=x/r
dus x=(r·h)/(h+r)

Is dit een verkeerde redenering? En waarom komt het dan juist uit?
Isabel
3de graad ASO - dinsdag 19 november 2002

Antwoord

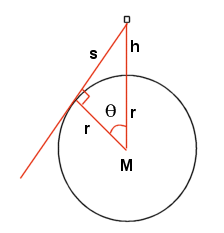
Laten we de h hoogte van de waarnemer noemen, en r de straal van de aarde.
Hierboven zien we de situatie.
Vanuit de waarnemer is een raaklijn aan de aarde te trekken, het punt waar deze raaklijn de aarde raakt, is de horizon van de waarnemer. Je kunt je al wel voorstellen dat hoe hoger je staat, hoe verder je horizon zal komen te liggen.

We moeten een uitdrukking vinden voor de hoek $\theta$ zoals deze in het plaatje aangegeven is.
Bedenkt dat de driehoek die ontstaat uit de lijnen 'r+h', 'r' en 's' een rechthoekige driehoek is.
zodoende geldt dat:
cos$\theta$=r/(r+h)

Vervolgens bekijken we hoe we de oppervlakte van een bol-oppervlak kunnen berekenen. Hierbij hoort onderstaand plaatje:

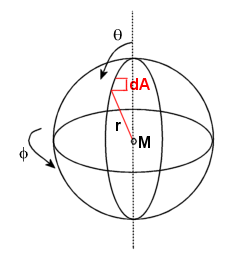
Ga er voor het gemak even vanuit dat de waarnemer zich pal boven de noordpool bevindt. Een punt op de (aard-)bol kan aangegeven worden met behulp van 2 hoeken, $\theta$ en f.
$\theta$ is de hoek gerekend vanaf de noordpool richting de evenaar (de breedtegraad), en f is de hoek langs de evenaar gemeten (de lengtegraad).
Een klein oppervlakje dA kan berekend worden uit z'n lengte maal z'n breedte.
lengte is r.d$\theta$
breedte is r.sin$\theta$.df

Dat de lengte rd$\theta$ is, is nog wel een keer in te zien. Maar hoe kom je bij de breedte aan die factor sin$\theta$? Wel, doordat naar de polen toe de stukjes in oost-west richting alsmaar korter worden. Dus moet je corrigeren voor de breedtegraad waarop je je bevindt.

dA=d(LENGTE).d(BREEDTE)
=(rd$\theta$).(rsin$\theta$df)
=r²sin$\theta$d$\theta$df

Dus de oppervlakte van het bolgedeelte behorend bij hoek $\theta$ is:
O=$\int{}\int{}$r²sin$\theta$d$\theta$df
waarbij de ene integraal loopt van f=0 naar f=2 $\pi$
en de andere van $\theta$=0 naar $\theta$=$\theta$
bedenk tevens dat r=constant dus mag buiten de integraal:

O=r²$\int{}\int{}$sin$\theta$d$\theta$df
=2 $\pi$ r²$\int{}$sin$\theta$d$\theta$
=2 $\pi$ r²[-cos$\theta$]^$\theta$₀
=2 $\pi$ r²(1-cos$\theta$)

We hadden reeds berekend dat cos$\theta$=r/(r+h), vul dit in

O=2 $\pi$ r²(1-r/(r+h))=2 $\pi$ r².h/(r+h)

Hieraan zie je dat wanneer de waarnemer zich op oneindige hoogte bevindt, de oppervlakte van de zichtbare bol gaat naar 2 $\pi$ r², en dit is precies de opp. van een halve bol.
Gaat h naar nul, dan gaat ook de zichtbare oppervlakte naar nul.

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 november 2002

Re: Oppervlakte bolkap