WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Perspectiefprojectie van ellips

Stel, ik maak een ovaal; deze ovaal word vanaf 5 meter bekeken. De persoon die deze ovaal bekijkt, heeft een ooghoogte van 1.75 meter. Wat zijn dan de afmetingen van de ovaal wil deze persoon de ovaal OPTISCH als een cirkel ervaren?
Misschien makkelijker...neem een cilinder in gedachte met een diameter van 30 centimeter, deze staat onder een hoek van 25 graden; hoe groot word de ovaal die er onstaat wanneer de cilinder het "platte vlak" doorkruist.

Mischien niet helemaal duidelijk, maar de bedoeling is om een ovaal te maken, en ik wil dan weten hoe je berekend wat de kijkhoogte in relatie met de afstand (vanwaar de ovaal bekeken word) moet zijn om de kijker (met 1 oog) een perfecte cirkel te laten ervaren...en daaruit zou dan dus ook de grootte van de ovaal te berekenen moeten zijn...

Ik kom er zelf niet uit, ik hoop dat jullie een antwoord op mijn vraag hebben
Johan
Student hbo - dinsdag 19 november 2002

Antwoord

Hoi,

Voor je cilindervraag vind je makkelijk dat de korte as van je ellips 30cm is en de lange as 30/cos(25°).

In het plaatje vind je de situatie met een kijkoog op hoogte h en afstand d van het centrum van je ellips.

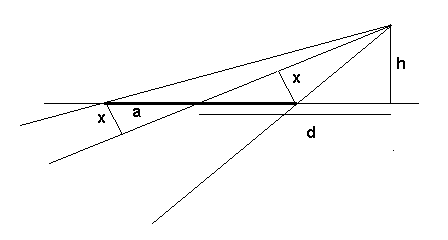
We veronderstellen dat de assen 2a en 2b lang zijn met ab. Enkel langs de recht door a kunnen we een cirkel krijgen.
De as met lengte 2b vervormt dan niet en x is het beeld van a. We zien dat x/a=h/d. Voor x=b hebben we dus: h/d=b/a.

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 november 2002