WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

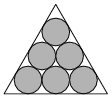
Efficientie verpakking

Hoi, ik heb een klein probleempje. ik heb een gelijkzijdige driehoek met daarin zes cirkels. deze zitten er in zo dat het driehoek maximaal gevuld is. mijn vraag is nu hoe ik aan de percentage cirkels kom dat wordt ingenomen door het driehoek? ik kom uit op 39.4% maar volgens mij kan dat niet kloppen.

Ik hoop dat jullie mij kunnen helpen!

bedankt
Sooner
Leerling bovenbouw havo-vwo - zaterdag 9 februari 2008

Antwoord

Als je naar het plaatje kijkt dan zal die 39.4% wel niet kloppen:

Volgens mij moet je de totale oppervlakte van de 6 cirkels delen door de oppervlakte van de gelijkbenige driehoek.

O(cirkel)=$\pi$r²
O(gelijkzijdige driehoek)=¹/₄√3·z²

Neem bijvoorbeel z=2 en bereken r. Je kunt daarbij gebruik maken van de symmetrie en de grootte van de hoeken.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 9 februari 2008