WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Arccos handmatig berekenen

Beste wisfaq,
Een tijd geleden heb ik een vraag gesteld over het handmatig oplossen van een goniometrische functie in de vorm van:
arcsin(cos($\pi$/3))
of in het algemeen geschreven: arcsin(cos(a))

Ik kan nu voor de arcsin alle hoeken oplossen en wel door de volgende theorie:

ik heb een rechthoekige driehoek met schuine zijde 1 (eenheidscirkel) en hoeken a, b, c
lijn a b is horizontaal (tevens cos(A)
lijn b c is verticaal (tevens sin(A)
lijn c a is de schuine zijde

uit deze figuur kan ik het volgende opmaken:
cos(A)= a/s= cos(A)/1 = cos(A)
sin(C)= o/s= cos(A)/1 = cos(A)

dus sin(C)=cos(A)!!

dus bijv.
arcsin(cos($\pi$/3))=arcsin(sin($\pi$/2 - $\pi$/3))=
arcsin(sin ¹/₆ $\pi$)= ¹/₆ $\pi$
of het antwoordt positief of negatief is, kan bepaald worden door te kijken in welke kwadrant de hoek gemaakt wordt, voor 1 en 4 kwadrant positief
voor 2 en 3 kwadrant negatief

ik probeer op gelijke wijze de arccos(sin(a)) op te lossen, maar dat lukt me niet.....
kunt u me hiermee helpen?

een voorbeeld waar het wel lukt is bijvoorbeeld:
arccos(sin$\pi$/3)= arccos(cos ((¹/₂ - ¹/₃)$\pi$)=1/6$\pi$ (is dit toeval dat het lukt?)

maar bij arccos(sin-$\pi$/3)= lukt dat niet

en voor de volledigheid:
arccos(sin-3$\pi$/4)? (deze moet in ieder geval tussen o,5$\pi$ en $\pi$) liggen)

hopelijk is duidelijk wat mijn vraag is.....

mvg,

Carlos

carlos
Student universiteit - maandag 28 januari 2008

Antwoord

Ik zou eerder kiezen voor grafieken. Het probleem is natuurlijk dat arcsin en arccos alleen op een bepaald (en verschillend) domein gedefinieerd zijn.

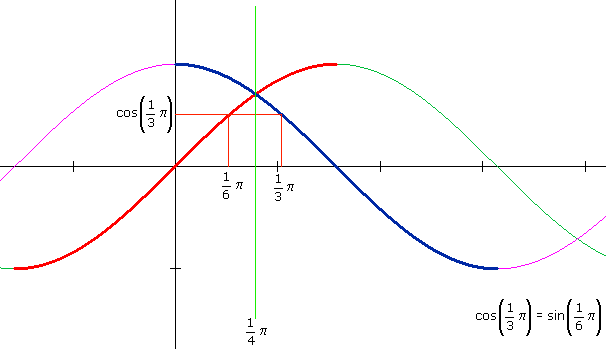
De twee punten liggen symmetrisch t.o.v. de lijn x=¹/₄$\pi$

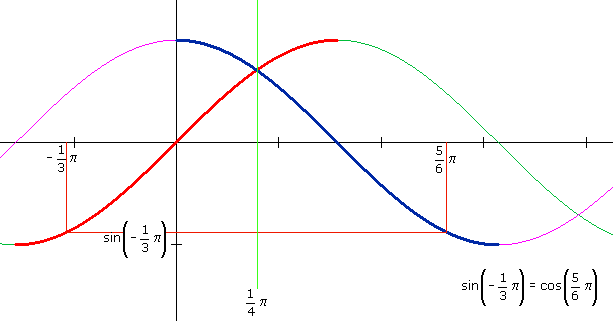
De twee punten liggen symmetrisch t.o.v. de lijn x=¹/₄$\pi$

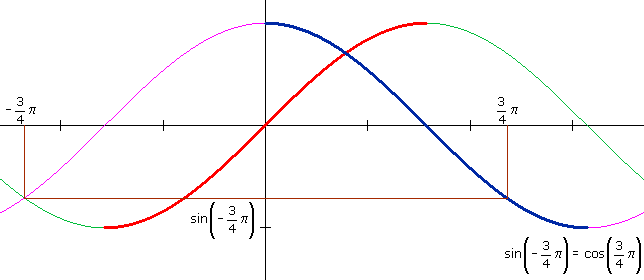
Dat lijkt iets anders maar is toch weer hetzelfde...

Hopelijk kom je daar verder mee.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 28 januari 2008