|
|
|
\require{AMSmath}



Oplossen goniometrische vergelijking
Beste mensen van Wisfaq,
Hoe los ik de volgende vergelijking op:
cos 2x = 0,5.
De volgende stap moet zijn: 2x = (1/3)p + 2kp, maar ik begrijp niet hoe ik hier aan moet komen...
Alvast bedankt!
Birgit
Birgit
Student universiteit - zondag 27 januari 2008
Antwoord
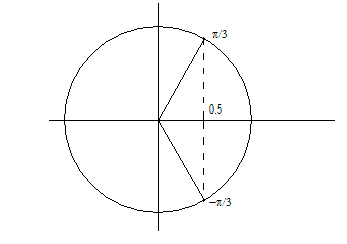
Je weet dat de cos(p/3) = 1/2
Ook de tegengestelde hoek heeft dezelfde cosinus, dus cos(-p/3) = 1/2
Ook de hoeken die een veelvoud van 2p (= 360°) van deze hoeken verschillen, hebben dezelfde cosinus.
Als je dus de vergelijking cos(2x) = 0.5 moet oplossen, kun je stellen dat
2x = p/3 + 2kp of 2x = -p/3 + 2kp
en dus
x = p/6 + kp of x = -p/6 + kp

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 27 januari 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










