|
|
|
\require{AMSmath}



Stelling van Ceva
Waarom geldt bij de stelling van ceva dat de verhoudingen bij 3 hoektransversalen gelijk aan 1 moeten zijn.
Waarom 1 en niet b.v. 0,5.
Het bewijs voor gelijk aan 1 begrijp ik wel.
Maar weet u ook waarom 1 en niet 0,5.
Mis ik iets??
a.deni
Leerling bovenbouw havo-vwo - maandag 12 november 2007
Antwoord
Beste A,
Je hebt het al eerder gehad over verhoudingen van hoektransversalen. Daarmee bedoelde je de verhoudingen van de afstanden van zo'n transversaal tot de benen van de hoek.
In de stelling van Ceva gaat het over de verhoudingen waarin concurrente transversalen de zijden van een driehoek verdelen.
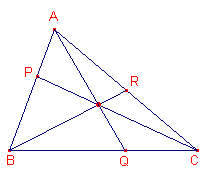
Er geldt:
(AP/PB)·(BQ/QC)·(CR/RA)=1
zie figuur 4 in:
http://www.pandd.demon.nl/transvers.htm#0
Als je begrijpt hoe je kan bewijzen dat het product van die verhoudingen 1 is, hoe kan het dan 0,5 zijn?
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 12 november 2007
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|









