|
|
|
\require{AMSmath}



Hoek tussen 2 vlakken
Hallo wisfag,
Hoe bereken ik de hoek tussen 2 snijdende vakken zijnde:
$\alpha$: -x+y+z=1 en $\beta$:x-y+z=1 ?Toch wat moeite mee?
Vriendelijke groeten
Rik Le
Ouder - zaterdag 27 oktober 2007
Antwoord
Beste Rik,
De hoek tussen twee vlakken kan je berekenen door de hoek te berekenen tussen de normaalvectoren.(loodrecht op die vlakken)
De normaalvector van vlak ax+by+c=d is: (a,b,c)
Nu geldt: 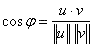
Hierin zijn u en v de beide normaalvectoren.
In de teller staat het inwendig product .Je neemt daarvan de absolute waarde, omdat je onder de hoek tussen twee lijnen altijd de kleinste hoek kiest.
In de noemer staat het product van de absolute waarden van u en v.
Zie voor een voorbeeld:Zou het zo lukken?
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 27 oktober 2007
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|