WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

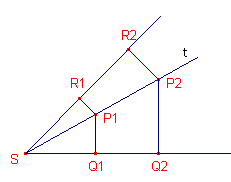
Ceva

Hoe bewijs je dat een willekeurige lijn door het snijpunt van 2 lijnen en 2 punten daarop met de projecties op de 2 lijnen een constante verhouding hebben.
B.V. P1Q1:P1R1 = P2Q2 : P2R2 .
A.deni
Leerling bovenbouw havo-vwo - zaterdag 20 oktober 2007

Antwoord

Beste A.

Ik neem aan dat je doelt op een hoektransversaal.
Een mooie uitleg met bewijs vindt je hier:
http://www.pandd.demon.nl/transvers.htm#0

DSQ₁P₁~DSQ₂P₂®P₁Q₁/P₂Q₂=SP₁/SP₂
(Want P₁Q₁ en P₂Q₂ zijn de kortste afstanden van t tot de lijn door S en de punten Q en dus loodrecht)
Analoog vinden we:
R₁P₁/R₂P₂=SP₁/SP₂
Gevolg: R₁P₁/P₁Q₁=R₂P₂/P₂Q₂

Je moet natuurlijk wel nog netjes bewijzen dat die driehoekjes gelijkvormig zijn.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 oktober 2007