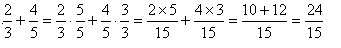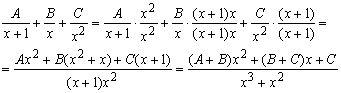WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Afsplitsen in A, B en C

waarom wordt er bij de opgave (x²+1)/(x³+x²) - A/(x+1) + B/x + C/x² A vervolgens vermenigevuldigd met C, C met A en B met B en A?

en waarom wordt in de noemer x³+x² onder verdeeld in x+1, x en x²?

alvast bedankt voor het antwoord
dyanth
Student hbo - maandag 8 oktober 2007

Antwoord

Nogmaals, beste Dyantha,

Je begint altijd de noemer te ontbinden in factoren.
De noemer is: x³+x²=(x+1)×x².
Dan kijk je hoeveel nulpunten er zijn in de noemer.
Hier: x=-1 en x=0 (twee keer).
Dan probeer je de functie te schrijven als: A/(x+1)+B/x+C/x².
Je gaat dan bepalen wat A, B en C moeten zijn door weer terug te werken naar de oorspronkelijke breuk. Daarbij vermenigvuldig je A met x², B met x(x+1) en C met (x+1).
Je doet hetzelfde bij gelijknamig maken van breuken als je breuken wil optellen:

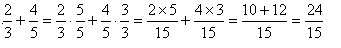
Nu weer terug naar jouw functie die je wil breuksplitsen:

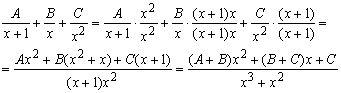
En dan moet gelden:
A+B=1; B+C=0 en C=1.

Zie ook: Breuksplitsen

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 8 oktober 2007