WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limiet van breuk met variabele in de exponenten

lim x-¥ ( 7x³ + 8x⁵ + 2^(2x) ) / (1 + 4^(x-1) )

Wel, ik zou zeggen dat het enige nuttige wat we nodig hebben is:

( 2^(2x) ) / ( 4^(x) ) = 1 als x naar oneindig gaat...

Maar het antwoord moet 4 zijn. Hoe kan ik een limiet berekenen als er een variabele in de exponenten staat?
Ronald
Student universiteit - zondag 16 september 2007

Antwoord

Beste Ronald,

Op de middelbare school zeggen we meestal: Een exponentiële functie wint het altijd van een machtsfunctie.
Met standaard limieten wordt dat wat netter uitgedrukt met:

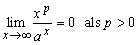
Nu kan je jouw functie opsplitsen in:
(7x³+8x⁵)/(1+4^x-1) en 2^2x/(1+4^x-1).
Die +1 mag je voor grote x verwaarlozen, en dan blijft dat enige nuttige wa je al zag over.
Genoeg??
Groeten,

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 september 2007

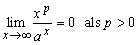
Re: Limiet van breuk met variabele in de exponenten