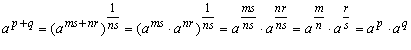WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Berekenen zonder ZRM

Hey, waarschijnlijk zie ik iets eenvoudigs over het hoofd maar ik slaag er niet in om het resultaat van (Ö15-Ö5)² te berekenen (moet zonder ZRM gebeuren). Dus waarschijnlijk zal ik het een en ander moeten vereenvoudigen.

Ik zal even mijn klad weergeven:
= 20 + 2 x Ö75
= 20 + 2 x 10Ö3
= 10 ( 2 - Ö3)

Los van deze oefening wordt ook gevraagd om het bewijs te geven van hetvolgende:
1. "a Î strikt positieve reële getallen "p,q Î: a tot de macht p + q= a tot de macht p x a tot de macht q
2. "a,b Î strikt positieve reële getallen " p Î(zonder 0): atot de macht p = b tot de macht p Ûa=b
Johnny
Student Hoger Onderwijs België - zondag 26 augustus 2007

Antwoord

Beste Johnny,

Je eerste vraag:Vereenvoudig: (Ö15-Ö5)²
Je eerste stap moet zijn: 20-2Ö75
Je tweede stap moet zijn: 20-2x5Ö3 =20-10Ö3
En de laatste stap is weer goed!
In een exact antwoord moet je niet te vereenvoudigen wortels laten staan, dus je antwoord is zo goed.

De twee bewijzen die je vraagt zijn van een heel ander kaliber!
Ze staan prachtig uitgewerkt op onderstaande site, waar nog veel meer moois is te vinden.

http://www.math.unl.edu/~webnotes/classes/class16/Fact3.htm

Het eerste bewijs is gebaseerd op:
p=m/n en q=r/s, dan: p+q=(ms+nr)/ns, waarbij m,n,r en s gehele getallen zijn, r en s positief.
Nu werk je met gehele getallen, waarvoor de regel al bekend is.

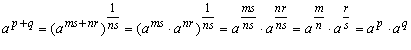
Voor het tweede bewijs stel je weer p=m/n
A=(a^m)^1/n =(b^m)^1/n
Vervolgens: Aⁿ=a^m=b^mÛa=b
Voor het gehele bewijs zie ook de gegeven site.

Hoop je hiermee van dienst te zijn geweest.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 27 augustus 2007