WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Koorde-cirkelboog-probleem

Het betreft een (wertuig)bouwkundig probleem.
Ik heb twee balken (of strippen) tot mijn beschikking.
Nummer 1 met lengte a en nummer 2 met lengte b.
Lengte a is een stuk langer dan lengte b.
Lengte a wordt met beide uiteinden aan de uiteinden van b bevestigd. a krijgt hierdoor een boogvorm.
Hoe bereken ik nu de hoogte van de boog(a)in het midden t.o.v. balk b? Dit is dus het verschil tussen de straal en de afstand vanuit het denkbeeldige midden tot aan de koorde (dikte materiaal verwaarloosbaar). In mijn benadering stuit ik steeds op 2 onbekenden met 1 oplossing. Onbekend zijn immers de straal en de hoek van de denkbeeldige cirkel.
A. Ver
Docent - woensdag 6 november 2002

Antwoord

Hoi,

Als a flexibel en veerkrachtig is (zoals een bladveer) en b (oneindig) stijf, dan kunnen we dit (benaderend) modelleren als een koorde van een cirkel met lengte b en een cirkelboog op die koorde met lengte a. a en b zijn strikt positief. (Hypothese fysisch te valideren...)

Op http://mathworld.wolfram.com/Segment.html vind je een aantal nuttige formules. Met de grootheden zoals gedefinieerd in de figuur:

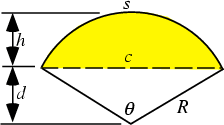
c = 2R.sin(q/2) = b
s = R.q = a

zodat 2.sin(q/2)/b=q/a
of sin(q/2)-b/a.(q/2)=0 (1)

Met x=q/2 moet je dus y=sin(x) en y=b/a.x snijden op [0,p]. Dit moet je numerisch oplossen. Voor ba vind je altijd precies 1 oplossing. Met q=2x en R=a/q heb je dan ook q en R.

Verder hebben we:
d = R.cos(q/2)
en h = R-d.

Tot zover de wiskundige aanpak...

Nu de ingenieursaanpak:
Als a@b, dan kan je de situatie zien als een driehoekje met hoogte h. Hierbij hebben we: (a/2)²=(b/2)²+(h)², waaruit: h = sqrt(a²-b²)/2.

Als dit niet nauwkeurig genoeg is, kan je voor a@b zien dat x klein is, en dan is sin(x)@x-x³/3 en cos(x)@1-x²/2. Hiermee kan je dan een andere benadering bepalen voor h in functie van a en b. Meer rekenwerk, misschien beter... Valt te bestuderen.

Als b stijf is en a is een koorde dit 'hangt' onder invloed van de zwaartekracht, dan vervalt onze hypothese: dan heb je een ketttinglijn. Als b ook vervormd, dan moet je rekening houden met de elasticiteitsmoduli, veerkonstanten etc. Hiervoor moet ik een cursus sterkteleer erbij nemen...

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 november 2002