WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Conflictlijn van cirkel 1 en cirkel 2 in cirkel 1

Gegeven zijn de cirkels c1 en c2

a) Bewijs dat de conflictlijn van c1 en c2 een ellips is.
b) Teken de conflictlijn van c1 en c2

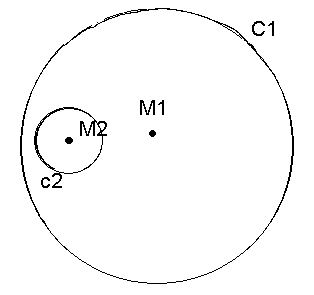
Het is vooral het tekenen van de conflictlijn waar ik mee zit, hoe moet ik nou precies weten hoe die ellips loopt? Is er misschien een manier om het probleem terug te brengen tot iets simpelers?
Nemi
Leerling bovenbouw havo-vwo - zaterdag 23 juni 2007

Antwoord

1) Als P een punt van die conflictlijn is, dan ligt P dús evenver af van beide cirkels. Laten we die afstand d noemen. Als cirkel C1 straal a heeft en cirkel C2 straal b, dan is de afstand van P tot M1 gelijk aan a-d en de afstand van P tot M2 gelijk aan b+d.
Dan geldt dus dat PM1 + PM2 = a-d + b+d = a+b en omdat a en b vaste getallen zijn, is de som a+b ook een vast getal.
Conclusie: PM1 + PM2 is een vast getal, en dat is precies wat de definitie van een ellips vraagt. M1 en M2 treden dus op als de brandpunten van de ellips.

2) Teken met middelpunt M1 een tweede cirkel C3 met straal a+b.
Neem nu op C3 een willekeurig punt Q en verbind dit punt met M1 en M2.
Teken de middelloodlijn van QM2 en snijd deze met lijnstuk QM1.
Dit snijpunt is nu een punt van de ellips in wording.
Door dit punt te spiegelen in de lijn M1M2 krijg je er meteen een tweede punt gratis bij. Het herhalen van deze constructie door steeds een ander punt Q te nemen, levert vrij snel een redelijke ellipsvorm op.

3) Deze constructie moet toch in elk meetkundeboek te vinden zijn? Als je toevallig werkt met Getal en Ruimte, dan vind je de opgave op blz. 153 als nummer 22. Zelfs de tekening is precies hetzelfde, dus...........?!

MBL

MBL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 24 juni 2007