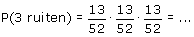WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kaarten uit een compleet spel met terugleggen

Ik heb vorig jaar voor het laatst kansberekenen gehad, en ik zit nu op een HBO opleiding, waarbij het uitleg boek dat ze hebben gegeven echt heel erg onbegrijpelijk is.

Je trekt met teruglegging 3 kaarten uit een compleet spel.
Bereken de kans dat het 3 ruiten zijn.
Bereken de kans dat de eerste kaart een ruiten is, 2e een harte en 3e een schoppen.
Het een ruiten, een harten en een schoppen zijn.
Het niet één ruiten, en één harten en één schoppen zijn.
Ik kom echt niet uit deze vraag: (waarschijnlijk is hij heel erg makkelijk, maar ik weet gewooon niet meer hoe ik hem moet uitrekenen)
Anne
Student hbo - dinsdag 19 juni 2007

Antwoord

Je hebt 52 kaarten, waarvan steeds 13 van elk soort.

A.
De kans dat de eerste kaart een ruitenkaart is is gelijk aan het aantal ruitenkaarten gedeeld door het totaal aantal kaarten. De kans dat de tweede kaart ook een ruitenkaart is is gelijk aan het aantal ruitenkaarten... enz.

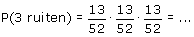
B.
De kans dat de eerste kaart een ruitenkaart is is gelijk aan het aantal ruitenkaarten gedeeld door het totaal aantal kaarten. De kans dat de tweede kaart een hartenkaart is is gelijk aan het aantal hartenkaarten... enz.

C.
Dit is iets lastiger omdat er verschillende rangschikkingen (volgordes) zijn die zouden kunnen. Een gedegen 'aanpak' is om de kans op één zo'n volgorde uit te rekenen (hebben we al gedaan bij B) en deze kans dat te vermenigvuldigen met het aantal rangschikkingen die je kan maken met 1 ruiten, 1 harten en 1 schoppen.

D.
De kans op niet 'één ruiten, en één harten en één schoppen' is de complementaire kans van wel 'één ruiten, en één harten en één schoppen'. Deze laatste kans heb je uitgerekend bij C.

...en dan ben je er wel zo'n beetje denk ik.

Zie ook 1. Telproblemen en 2. Kansrekenen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 juni 2007