|
|
|
\require{AMSmath}
Re: Oppervlakte en inhoud berekenen van een octäeder
Nou ik snap het echt niet!?
mauric
Leerling bovenbouw vmbo - woensdag 23 mei 2007
Antwoord
De bovenhelft van je octaëder is een piramide met een vierkant grondvlak. De zijden van die piramide zijn allemaal 6 cm. Ok?
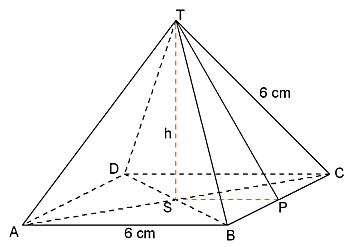
Voor de oppervlakte van de driehoeken en de inhoud van de piramide heb je lengte van TP nodig en de lengte van TS. TS noemen we de hoogte h.
De lengte van PT kan je berekenen met de stelling van Pythagoras. In de rechthoekige driehoek BPT weet je dat BP=3 en BT=6. Je kan dan de lengte van PT berekenen. Toch?
Als je de lengte van PT kent dan kan je in de rechthoekige driehoek SPT de hoogte h uitrekenen. Ook weer met de stelling van Pythagoras. Je weet PT (zie boven) en je weet SP=3.
De oppervlakte van een driehoek bereken je door 'een half keer basis keer hoogte'. In driehoek BCT is dat dan 1/2·BC·PT. Je weet BC=6 en PT heb je hierboven uitgerekend.
Je octaëder bestaat uit 8 van dat soort driehoeken, dus de totale oppervlakte is dan 8 keer de oppervlakte van driehoek BCT.
De inhoud van een piramide bereken je door 'één derde keer grondvlak keer hoogte'. In dit geval 1/3·Opp(ABCD)·h. Je weet Opp(ABCD)=36 en h heb je hierboven uitgerekend.
Je octaëder bestaat uit 2 van deze piramiden. De totale inhoud is dan 2 keer de inhoud van de piramide.
...en volgens mij ben je er dan... toch?
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 mei 2007
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 50895