|
|
|
\require{AMSmath}



De respons van de steekproef
Ik onderzoek de wensen en behoeften van de bezoekers van de site op het gebied van digitale toeristische informatievoorziening. Door middel van een online enquête.
· De werkelijke populatie is 1900.
· De steekproef is 1900 (alle contactpersonen zijn uitgenodigd voor een online enquête).
· De respons is 190 mensen = 10%.
Hoe betrouwbaar is de respons als je uitgaat van een betrouwbaarheidsniveau van 95%?
Hoe representief is die 10% voor de gehele populatie?
Ik zie wel formules voor steekproefmarge en steekproefgrootte, is er ook een formule voor de responsgrootte?
Ik wil de betrouwbaarheid, nauwkeurigheid en representativiteit aan kunnen tonen.
Alvast bedankt,
Lisa.
Lisa
Student hbo - maandag 21 mei 2007
Antwoord
Allereest kan je van jezelf zeggen dat je het maximale gedaan hebt wat je kunt doen. M.a.w. je hebt de hele populatie benaderd, beter kan dus niet.
Wat je uiteraard niet weet is of die respons representatief is. Dat kan je hieruit niet halen en is in het algemeen ook zeer lastig om dat in de vingers te krijgen. Representativiteit is wel aantoonbaar voor zover je van belangrijke kenmerken (bv geslacht) zowel in de populatie als in de steekproef aantallen kent. De praktijk leert dat representativiteit in het algemeen bij zo'n onderzoek niet valt aan te tonen.
De steekproefgrootte is niet zo'n goede benaming. Daarbij moet je denken aan de responsgrootte en die is bij jou 190.
Dat betekent dat je bij schattingen van percentages rekening moet houden met een onnauwkerigheid (=marge). Dat geeft aan hoever het steekproefresultaat maximaal af kan wijken van het bijbehorend percentage in de populatie (met 95% betrouwbaarheid).
De berekening van die marge gaat als volgt:
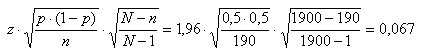
Die p is de het steekproefpercentage bij een bepaalde variabele. De laatste Ö is de correctie voor eindige popuaties. De uitkomst betekent dat je bij een percentageschatting uit de steekproef rekening moet houden met een onnauwkeurigheid van maximaal 0,067 (6,7%) met 95% betrouwbaarheid. That's all there is.
Met vriendelijke groet
JaDeX

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 29 mei 2007
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|