WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De gulden snede en zonnebloem

Hallo,

Ook ik maak een praktische opdracht over de gulden snede..

Ik heb eigenlijk een vraag, waar de wiskunde docenten geloof ik ook niet helemaal uitkomen. En helaas is mijn eigen docent nu met werkweek...

Onderzoek hiermee wat er gebeurt als een zonnebloem, vanuit het midden beginnend, ieder volgend zaadje b.v. over 180 graden (dus een fractie 0.5 van de 360 graden) gedraaid zou laten groeien. Leg duidelijk uit waarom het gebruik van breuken (1/5 · 360, of 3/11 · 360) geen goede tactiek voor de zonnebloem is. Let op: je uitleg moet betrekking hebben op alle breuken en dus niet op een paar concrete gevallen.

Ga na dat het gebruik van Phi of phi wel een goede 'pakking' oplevert. Tel hoeveel spiralen er linksom lopen en hoeveel er rechtsom lopen (pagina printen - dat is makkelijker tellen). Wat is het verband met Fibonacci? Van dit en het vorige onderdeel neem je uiteraard plaatjes op in je werkstuk.

Ik heb hier de vraag maar even letterlijk gekopieerd. Mijn vraag hierbij is als jullie misschien hier een antwoord en/of toelichting hebben?
Alvast bedankt!
Annegr
Leerling bovenbouw havo-vwo - donderdag 10 mei 2007

Antwoord

Met het Excelblad kan je onderzoeken hoe de verschillende zaden verdeeld worden. Maar bij ¹/₅ is de verdeling niet erg efficiënt:

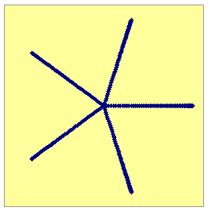
Je zou kunnen denken dat dit komt omdat ¹/₅·360° wel erg mooi uitkomt... Maar ook bij ³/₁₁ lijkt het niet erg te lukken:

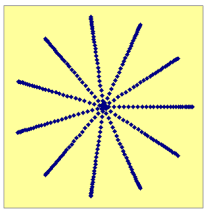
Zelfs bij 1/$\pi$ gaat het beter, maar uiteindelijk toch niet goed:

Met 1/$\phi$ gaat het een stuk beter:

De opdracht is dan om dit te verklaren en bij de laatste plaatje het aantal spiralen te tellen (links- en rechtsom). Bij de links kan over dit onderwerp nog veel meer informatie vinden.

Zie ook De gulden snede en de zonnebloem

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 12 mei 2007