WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

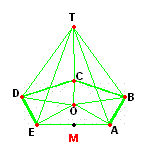
Formule voor de hoek tussen wanden van piramides met verschillende regelmatige

Ik wil een toren maken van multiplex met als basis een regelmatige n-hoek waarvan de wanden onder x graden staan (spitse piramide) met daarop een dakje met een helling van x graden (platte piramide). Hoe bereken ik de (gedeelde) hoek tussen de wanden cq. dakplaten? Is hier een formule voor?
Dennis
Iets anders - maandag 7 mei 2007

Antwoord

Hoi Dennis,

Ik teken even het voorbeeld van een vijfhoekig grondvlak.

neem OA=1 (voor de hoeken maakt dat niet uit)
1/AT = cos(x)
AT = 1/cos(x)

M is het midden van AE
OAM is een rechthoekige driehoek.
AM = sin(180°/n)

cos(ÐMAT) = AM/AT = cos(x)sin(180°/n)

om hem af te knotten zaag je driehoek ATE op de juiste hoogte af evenwijdig aan AE.

Lukt het hiermee? Groet. Oscar

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 mei 2007