WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Oppervlakte bol

Beschouwen we de doorsnede van een vlak evenwijdig met het XY-vlak en een bol met straal R en middelpunt de oorsprong.

Dan heeft deze bol vgl. x² + y² + z² = R². De cirkeldoorsnede heeft dan vgl. x² + y² = R² - C² als het vlak vgl. z = C heeft. Aldus heeft deze cirkel omtrek
2·Pi·ò(R² - C²).

Integreren we deze omtrek van -R tot R, dan verwachten we de oppervlakte van de bol uit te komen. Helaas:

ò2·Pi·Ö(R² - z²)dz gaande van -R tot R geeft R²·Pi²...wat niet gelijk is aan 4·Pi·R².

Wat doe ik fout?
Raph
Student universiteit België - zaterdag 21 april 2007

Antwoord

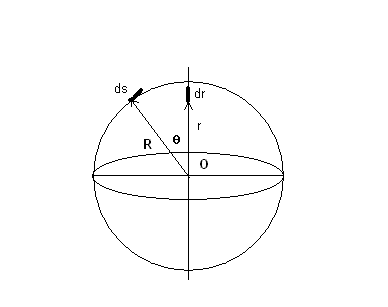
De denkfout die je waarschijnlijk maakt, is dat wanneer je integreert van -R tot +R, je bolschilletjes aan het optellen bent met omtrek 2pÖ(R²-r²) en dikte dr. Die omtrek is juist, maar de dikte is niet juist.
Wanneer je naar bovenstaande tekening kijkt, zie je dat met toenemende hoogte (vanaf de oorsprong gezien) het stukje ds schever loopt.
Dat betekent dat de breedte van het bolschilletje steeds wat groter wordt.

Er geldt dat ds=dr/sinq
En sinq=Ö(R²-r²)/R

dit levert voor de opppervlakte:
O = _-Rò^R2p.Ö(R²-r²).ds
= _-Rò^R2p.Ö(R²-r²).R/Ö(R²-r²) dr
= 2pR_-Rò^Rdr
= 4pR²

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 april 2007