WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

VWO 2006 r2, v14, via sin etc aantonen waaraan een lengte gelijk is

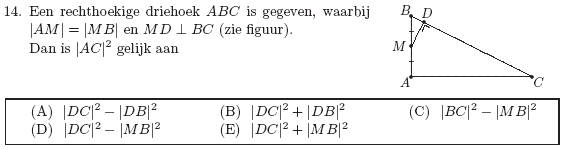
Een rechthoekige driehoek ABC is gegeven, waarbij |AM|=|MB| en MD ^ BC
Dan is |AC|² gelijk aan:
(a) |DC|²-|DB|²
(b) |DC|²-|MB|²
(c) |DC|²+|DB|²
(d) |DC|²+|MB|²
(e) |BC|²-|MB|²

Op vwo staat dat (a) de juiste oplossing is, maar ik versta niet hoe men hieraan komt.
http://www.vwo.be/vwo/vorige-edities/tweede-ronde-2007
Bart
3de graad ASO - zaterdag 14 april 2007

Antwoord

Voor 't gemak noem ik BC=a, AC=b en AB=c. Dus MB=¹/₂c.

Omdat driehoek ABC en driehoek DBM beide rechthoekig zijn en een hoek gemeenschappelijk hebben zijn deze driehoeken gelijkvormig.
Waaruit volgt dat c:BD=a:¹/₂c, oftewel BD=c²/(2a). Dus DC=a-c²/(2a)
Dan is DC²-DB²=(a-c²/(2a))²-(c²/(2a))²=a²-c²=AC²
(dat mag je alllemaal nog wel even netjes narekenen!)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 14 april 2007